Explain the representation of the CNOT gate in ZX-calculus

Question

In ZX-calculus, the CNOT gate is represented by this:

Can someone show me why this is true, using just the basic rewriting rules? All books/papers I have seen simply take it without proof, but I can't see why it is true.

Answer 1

I am going to assume that $|0\rangle$ is represented by 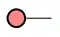, and $|1\rangle$ by .

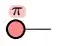Then, 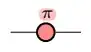represents the bit-flip, or NOT gate. What it does is: $|x\rangle\mapsto |x\oplus1\rangle$. This can be verified easily in the graphical calculus, using the "spider" rule:

and

Now, by definition, CNOT controls NOT: $|x_1,x_2\rangle\mapsto|x_1,x_1\oplus x_2\rangle$. In other words, if $|0\rangle$ is fed to the first qubit, the result is $|0\rangle$ on the first qubit, and the identity on the second. If it is fed $|1\rangle$, the result is $|1\rangle$ on the first qubit, and the gate NOT on the second one. Again this can be verified in the graphical calculus:

where the first equality is the "copy" rule, the second is the "spider" rule, and the last one is the fact that a rotation of angle $0$ is the identity.

Similarly:

where the first equality is the "$\pi$-copy" rule, and the second is the "spider" rule.