Generalising the standard quantum teleportation protocol: what are the possible unitaries?

Question

Consider the standard quantum teleportation scheme. Let the first register hold the state $\newcommand{\ket}[1]{|#1\rangle}\ket\psi$ to be teleported, and the second register be the one shared between the two parties. We can then summarise the protocol as follows:

1. Start with the state $\ket{\psi}_1\ket{0,0}_{23}$
2. Apply the unitary $U\equiv \operatorname{CNOT}(H\otimes I)$ between second and third register, thus evolving $\ket{00}$ to $\ket{\Psi^+}\simeq \ket{00}+\ket{11}$.
3. Apply $U^{-1}$ between first and second registers.
4. Measure the first two registers in the computational basis, and observe that for every outcome there is a local operation that can be applied to the third register that gives back $\ket\psi$.

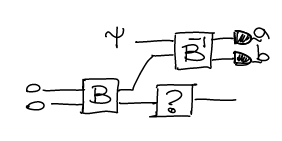
My question is about the choice of this specific unitary $U$: Consider the following generalisation of the teleportation scheme:

Here, we again start with $\ket\psi\otimes\ket{0,0}$, but now apply some unitary $B$ between second and third register and then $B^{-1}$ between first and second. We then measure the first two registers in the computational basis.

What are the possible unitaries $B$ such that this circuit works as a teleportation protocol? More specifically, for what choices of $B$ can we always find a unitary to apply to the third register to get back $\ket\psi$ regardless of the measurement results $a,b$?

Intuitively, $B$ must be some gate creating maximal entanglement between the qubits, but requiring that $B$ sends $|00\rangle$ to a maximally entangled state is also not enough. As a counterexample, we can consider the following $B$: $$B\equiv \begin{pmatrix} 0&0&1&0 \\ 1/\sqrt2 & 1/\sqrt2 & 0 & 0 \\ 1/\sqrt2 & -1/\sqrt2 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}.$$ It is not hard to check that with this choice teleportation is not possible, despite the two parties sharing a maximally entangled state. For example, the outcome $a=b=1$ projects the third qubit to $\ket0$, which contains no information about $\ket\psi$.

Answer 1

A necessary and sufficient condition on the unitary $B$ is that its columns all correspond to maximally entangled states.

There also does not need to be any relationship between the two unitaries labeled $B$ and $B^{-1}$ in your figure: as long as you start with a maximally entangled state of systems 2 and 3, and then measure systems 1 and 2 with respect to an orthonormal basis of maximally entangled states, there will be an operation (which depends on the measurement outcome) on system 3 that recovers the original state.

Moreover, this is all true not only for qubits, but for any single dimension $d$ shared by systems 1, 2, and 3.

These facts were proved by Werner:

R. Werner. All teleportation and dense coding schemes. Journal of Physics A 34: 7081-7094, 2001 (link to paper).

Answer 2

Looking back at this question, and with the hindsight of the other given answer, I realised the original framing is somewhat ill-posed. Thinking of teleportation with as in the figure with $B$ and $B^{-1}$ is a bit misleading: what matters is only that the two parties share a maximally entangled state, and there needs be no relation between the unitary used to generate said entanglement and the one used to perform the measurement with $|\psi\rangle$, the state to send over.

For a more thorough description of the protocol hinted at in this other answer, see also this other answer of mine.

The gist is: projecting on Alice's side onto a maximally entangled state of the form $|\Phi\rangle=(U\otimes I)|\Psi\rangle$ (where $|\Psi\rangle\equiv\sum_i |i,i\rangle$ is some reference maximally entangled state), results in Bob's holding the state $U^\dagger |\psi\rangle$, which is then easily corrected by applying the (local) unitary operation $U$.

Thus, if we can find a basis of maximally entangled state on which to measure on Alice's side, we're through. Luckily, this can be done taking the states $|\Psi_i\rangle\equiv(U_i\otimes I)|\Psi\rangle$ for any basis of unitary operations, thus satisfying $\operatorname{Tr}(U_i^\dagger U_j)=d\delta_{ij}$ with $d$ dimension of the space, and with $i=1,...,d^2$. Thus, measuring on this basis, gives some outcome $i$, corresponding to which Bob's state is $U_i^\dagger |\psi\rangle$. Alice sends Bob the value of $i$, and he uses it to apply the correct operation and recover $|\psi\rangle$.