Every qubit is a realization of some two-level quantum system with $\left| 0 \right\rangle$ and $\left| 1 \right\rangle$ states. These states have their energies $E_0$ and $E_1$ respectively. By solving the Schrödinger equation for the two-level quantum system one can show time evaluation of the $\left| 0 \right\rangle$, $\left| 1 \right\rangle$ and $\left| + \right\rangle$ states:
$$ \left| \psi_0(t) \right\rangle = e^{-i \frac{E_0}{\hbar} t} \left| 0 \right\rangle \\ \left| \psi_1(t) \right\rangle = e^{-i \frac{E_1}{\hbar} t} \left| 1 \right\rangle \\ \left| \psi_+(t) \right\rangle = \frac{1}{\sqrt{2}}\left( e^{-i \frac{E_0}{\hbar} t} \left| 0 \right\rangle + e^{-i \frac{E_1}{\hbar} t} \left| 1 \right\rangle \right)= \frac{e^{-i \frac{E_0}{\hbar} t}}{\sqrt{2}} \left(\left| 0 \right\rangle + e^{-i \frac{E_1 - E_0}{\hbar} t} \left| 1 \right\rangle \right) $$
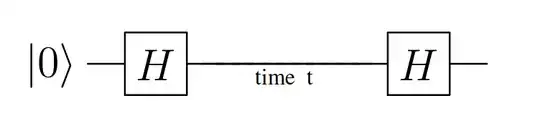
My question is about the relative phase $\varphi = e^{-i \frac{E_1 - E_0}{\hbar} t}$. This $\phi$ acts as a phase gate and changes the quantum state. Is this relative phase important and how in real quantum computers we should deal with it? One problem that I see is the following circuit:
After the measurement, the state should be $\left| 0 \right\rangle$, because $HH = I$. But If $t$ is such that the $\varphi = \pi$ then we will measure $\left| 1 \right\rangle$. We can forget about it if $\varphi(t) << \pi$ in the whole computational time. Otherwise, we should make sure that the time between gates should be $2\pi$.
Is this a problem and if yes how IBM, Google or etc. deal with this problem when constructing the circuits? How I understand the frequency $(E_1 - E_0)/\hbar$ value is important and for example, the ibmq_armonk qubit's frequency is equal to ~4.97428 GHz (qiskit_textbook), so should we take into account this value when we play with ibmq_armonk by using OpenPulse?