Are $\mathrm{cRz}$ with angle $\pi$ and $\mathrm{cZ}$ equal on the IBM Quantum Experience?

Question

I was trying to implement the 2-qubit Grover algorithm without the auxiliary bit. Before finding the gate symbol for the controlled $\mathrm{Z}$, I worked with the controlled $\mathrm{Rz}$. The gate glossary states: " $\mathrm{Z}$ is equivalent to $\mathrm{Rz}$ for the angle $\pi$". So I thought the controlled $\mathrm{Rz}$ with angle $\pi$ should be equal with the controlled $\mathrm{Z}$ gate. However, I get very different results in the browser state-vector representation.

So my question is, should they be equivalent?

Here are my circuits:

Answer 1

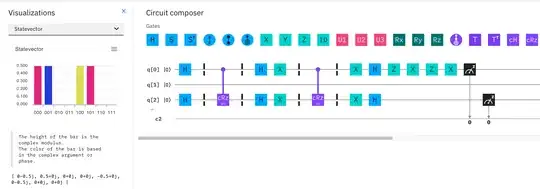
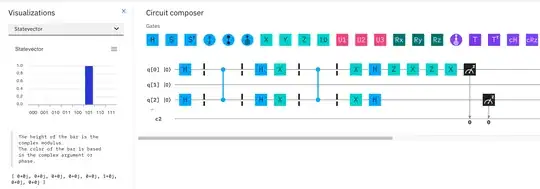
I realized that $\mathrm{Rz}(\lambda)$ is implemented in following way on IBM Q:

gate crz(lambda) a,b
{
  u1(lambda/2) b;
  cx a,b;
  u1(-lambda/2) b;
  cx a,b;
}

Setting $\lambda =\pi$, a matrix describing construction above is following: $$ \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & -i & 0 \\ 0 & 0 & 0 & i \\ \end{pmatrix} $$

This is not problem when the gate is not controlled as $i$ is a global phase, however, it matters for controlled gates.

I also checked that these values are really returned for computation basis states in state vector visualization on IBM Q.

Conclusion is that controlled $\mathrm{Rz}(\pi)$ is not equivalent to controlled $\mathrm{Z}$ on IBM Q.

Note that application of single qubit $\mathrm{Rz}(\pi)$ returns same results as single qubit $\mathrm{Z}$.

---

Solution:

To make controlled $\mathrm{Rz}(\pi)$ behave as expected, you have to put controlled global phase gate before $\mathrm{Rz}(\pi)$. You can do that by application single-qubit gate $\mathrm{U1}(\pi/2)$ on controlling qubit of $\mathrm{Rz}(\pi)$, i.e. $q_0$ in your case.