Meaning of generalized normal distribution

Question

I asked a version of this question over on Math.SX, and never received a response… perhaps it will be more appropriate here.

I'm looking at spectroscopic data (specifically a $T_2$ coherence decay curve of some NMR data). Normally, this data is fit to a single or multi-exponential decay to account for multiple components. However, I have a data set that fits best to a function with a power in the exponent near 1.4 (in between a Gaussian and single exponential decay).

Is there any physical meaning for generalized normal distribution functions? To elaborate on what I mean by "physical meaning", when working with spectroscopic absorptions, an an exponential decay (n=1) indicates a system with homogeneous broadening of lifetimes, while a Gaussian decay indicates inhomogenous broadening of lifetimes. What does a power between these two values indicate? Is there a precedent for using this sort of peak shape (or decay function in this case) in spectroscopic analysis?

--EDIT--

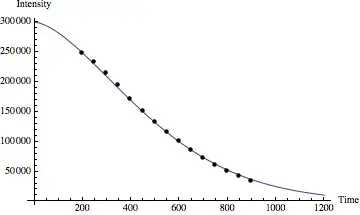
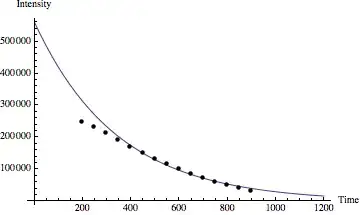
To demonstrate the phenomenon, here are a couple of sample curves with some data. The depressed points at the start may be an experimental artifact, but I'd still be curious to know if there is any physical precedent for the exponential power between 1 and 2.

$e^{-t/T_2}$

$e^{-(t/T_2)^{1.6}}$

Answer 1

Thanks to @user12262 for pointing me in the direction of the KWW function. After perusing that link and searching SciFinder for stretched and compressed exponential functions in relation to NMR, I ran across this paper (subscription required, sorry).

To (briefly) summarize the paper, the compressed exponential function, $e^{-kt^q}$, with $1 < q < 2$ can be represented as a distribution of Gaussian functions with different relaxation rates,

$$R_C (t) = \frac{1}{\pi} \int^∞_0 P_C(s; q)\, e^{−(sr^*t)^2} d\textrm{s},$$

where $R_C(t)$ is the observed decay curve, $P_C(s; q)$ is the probability distribution of Gaussian decays, $r^*$ represents some average value of the rate, and $s = r/r^*$. As the value of $q$ approaches 2, the distribution function approaches a delta spike (as one would expect).

In the case of NMR $T_2$ decays, this most likely represents a distribution of relaxation couplings (e.g. interactions with 1, 2, 3, etc. other nearby spins).