Speed of sound at temperatures below 0 °C

Question

How can the speed of sound be calculated for temperatures below 0 °C (down to -40 °C)?

Does the calculation $v=331\ \frac{m}{s} + 0.6 \frac{m}{s°C} \times T$ still hold (where T's unit is °C)?

Answer 1

The speed of sound in an ideal gas is given by

$$a = \sqrt{\gamma R T}$$

Where $\gamma = \frac{C_p}{C_v}$, $R$ is the specific ideal gas constant and $T$ is the absolute temperature.

Taking standard values for air, this makes a graph like this: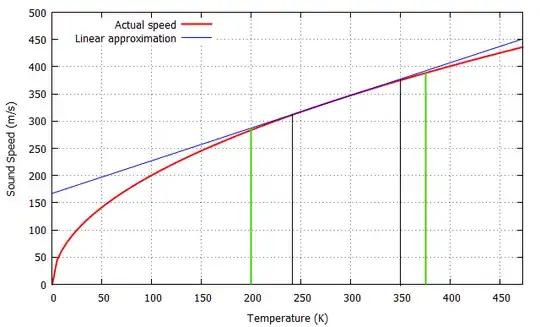

The linear approximation is plotted by your formula, $a = 331\ \frac{m}{s}\ +\ 0.6 \frac{m}{sK} (T - 273\ K)$, with the 273 K to convert it to the Kelvin scale.

As you can see, the linear approximation is nearly equal to the actual value in the range marked by the two black lines, from $T \approx 240\space\mathrm{K}$ to $T \approx 350\space\mathrm{K}$.

If you don't care about accuracy so much, you could even stretch your definition to $T\ \epsilon\ [200\space\mathrm{K},375\space\mathrm{K}]$, as shown by the green lines.

The error is:

• $\approx +1.3\%$ at $T=200\space\mathrm{K}$
• $\approx +1.0\%$ at $T=375\space\mathrm{K}$

As seen in the following graph of the percentage error of your approximation between $173\space\mathrm{K}$ and $473\space\mathrm{K}$.

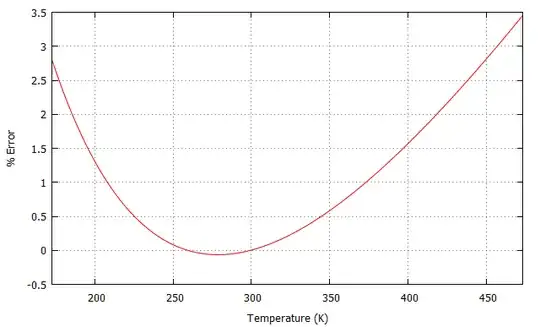
Of course, at low temperatures air doesn't behave like an ideal gas, so it all breaks down, but for the purposes of this question, I believe it's a fair assumption.

Answer 2

Wikipedia gives the formula $c_{air}=331.3\sqrt{1+\frac {T(^\circ C)}{273.15}}$, valid anywhere the ideal gas law is valid. The expression you quote is given at the first two Taylor series terms.

Answer 3

I don't know about your formula, but the speed of sound is proportional to the square root of the absolute temperature (for ideal gases, and approximately so in air).

Answer 4

In absolute zero, the molecular vibration is in its least possible extend. Therefor it is almost impossible to fluctuate under the influence of sound wave. Imposing any form of energy including sound energy will cause to increase in temperature . in supposed situation(Absolute Zero ) and a source that keeps the situation stable, sound would not be transmitted!!!