Feedback on the paper, 'CCC-predicted low-variance circles in CMB sky and LCDM' by V. G. Gurzadyan and R. Penrose

Question

Ref: CCC-predicted low-variance circles in CMB sky and LCDM

To all cosmology / theoretical physics / related or similar researchers and academics,

Roger Penrose's Conformal Cyclic Cosmology (CCC) proposes that low-variance circles in the Cosmic Microwave Background (CMB) are remnants from previous aeons. However, this prediction has been met with criticism. Given the detailed analysis of CMB data under the standard ΛCDM model, what are the key arguments against the existence of these low-variance circles as predicted by CCC?

Answer 1

Especially one of the authors is famous but the research of these CMB circles produced before the Big Bang resembles the research of crop circles produced by extraterrestrial aliens. In reality, the actual number of such "strong enough circles" is exactly what the statistical predictions based on standard cosmological models predict. It has to be so.

The authors have posted several papers with almost the same content and they're slightly changing the message. For example, in the newest paper you mentioned, they try to place their "new effects" in the large-$L$ region (low angular separation or apparent radii of the circles).

However, the fundamental flawed content remains unchanged. It's a simple mathematical fact that the excess of arbitrary spherically symmetric "special patterns" that can be described by a quadratic score $$\int d \theta_1 d\phi_1\, d\theta_2 d\phi_2 K(\theta_1,\phi_1,\theta_2,\phi_2) \Delta T(\theta_1,\phi_1)\Delta T(\theta_2,\phi_2)$$ and the Penrose-Gurzadyan "concentric circles" surely belong to this category (they haven't studied any non-Gaussianities, and even if they had, none of them are detectable in the measured WMAP spectrum as of today, anyway) - is inevitably included in the power spectrum as a function of $L$. For a simple proof, see

http://motls.blogspot.com/2010/12/why-penrose-and-gurzadyan-cannot-see.html

The kernel of their quadratic score $K(\hat n_1,\hat n_2)$ may be expressed as an operator acting on functions of $S^2$, the celestial two-sphere, and if this operator (e.g. if their rule to detect circles) is spherically symmetric, it has to be a function of $L^2$ only which means that this whole operator may be fully described by the eigenvalues it has when acting on $L^2$ eigenstates. In other words, it is fully encoded in the WMAP spectrum as a function of $L$.

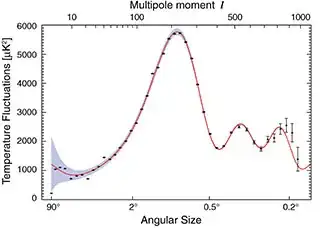
The WMAP spectral curve knows everything about the abundance of arbitrary patterns as long as this abundance may be described by a spherically symmetric score that is bilinear in $\Delta T$.

So one doesn't have to look at the particular data to be sure that the authors are misleading themselves. What they write about the excess, relatively to the predictions of the famous WMAP curve included on the picture above, is as impossible as $2+2=5$.

Before I admitted to myself that such famous authors (or one of them) could be ignorant about basic methods linked to the spherical harmonics, I wrote two texts speculating that they rediscovered something that is actually valid. One of them was:

http://motls.blogspot.com/2010/11/what-penrose-and-gurzadyan-have.html

But I no longer think that the article above is relevant. Their methodology is way too rough and unrefined for them to rediscover the things I thought that they rediscovered.

As long as one defines the "score" quantifying the number of concentric circles with various properties in terms of squared temperature differences in various pairs of the skies, this "score" is fully included in the WMAP spectrum that depends on $L$, and because this spectrum beautifully agrees with the predictions of the LCDM standard cosmological model, there's no room for some "improvements".

Independently of this basic mistake, I am surprised how incredibly superficial analysis they want to be making. They just want to answer the question "too many concentric circles Yes/No", and moreover, they give a wrong "Yes" answer to this question (by cherry-picking and irrationally overemphasizing some vaguely defined circles they like, without doing a proper statistical scrutiny of well-defined properties of the WMAP maps). Meanwhile, proper cosmology is predicting and testing whole detailed functions of $L$ with many bumps etc. - something that they're extremely far from addressing. The idea that they could compete with the standard cosmological model, without saying iota of valid things about the WMAP spectral curve, is preposterous.

Also, the mechanism of the proposed cyclic cosmology couldn't work to produce the alleged patterns. Incredibly enough, the main mistake that Penrose et al. do is a wrong Penrose diagram (note that the same name appears twice) for a Big Bang Cosmology. There can't be any "non-inflating" cosmology that has this big volume "before the Big Bang". If one wants to extend the diagram in this way, it's inevitable to include some very fast expansion of space that is inflation - at least when it comes to its consequences for the spacetime geometry. One should then ask what this inflation-like evolution of the geometry was caused by. And all known legitimate solutions are "morally" versions of inflation; it has to be so. I discussed these matters here:

http://motls.blogspot.com/2010/11/penroses-ccc-cosmology-is-either.html

So in my opinion, the authors have to get a failing grade in modern cosmology. Moreover, I am somewhat afraid that especially Penrose has to have understood the spherical harmonics calculus by now and he's defending the indefensible partly in order to promote a popular book he no longer wants to scratch (even though an honest scientist definitely should) - and this book is based on similarly incorrect statements.

Answer 2

It's very easy to go wrong in analyzing microwave background maps for this sort of signal. In particular, unless you're quite used to doing this sort of analysis, it's easy to make mistakes in calculating the probability of getting a false positive -- that is, of seeing patterns like the ones you're looking for, even if the standard model is correct.

I haven't reproduced the calculations myself (although I've done a number of very similar analyses in the past), but I have read papers by various other people arguing that the original result was incorrect. All of these papers present very clear and cogent explanations of the correct way to do this analysis and point out errors in the original analysis, which would have precisely the effect of inflating the statistical significance (by reducing the computed false-positive probability). Moreover, the rebuttals are written by people with extensive experience doing this sort of analysis, while the original paper was written by people with no such experience.

I conclude that there's no convincing evidence in support of the Gurzadyan-Penrose model. As far as I can tell, there's essentially complete consensus among experts in the field that this is the correct conclusion.

Answer 3

Since the first paper that I associate the circles with the voids.
in the paper, about Fig 4

The distortions could be the result of ... or more likely, ...Indeed, the presence of giant voids could particularly influence such images Gurzadyan V.G., Kocharyan A.A. (2009)

The concentric features reminds me a X-ray crystal diffraction pattern. It can trace a spatial volumetric regularity present in the creation of the photons of the CMB.
goggle for images of "X-ray crystal" and compare with Figs 4 and 5.
I think that this viewpoint is not allowed by the current mainstream cosmological model.
If you want to understand what it can trace, or not, one must ignore any preconceived model and start with the data analisys and discover if it was properly done, and then answer to the question: can it trace a volumetric regularity ?
If the answer is 'yes' or a 'may be' I can assure that a cosmological model already exists.
(not the CCC one)