A question was asked over at EE.SE recently which I tried to answer, but much of my answer was speculative. I'm hoping someone here can help my ignorance.
In electronics design, there are four physical quantities of interest: voltage, flux, charge, and current. If you have four things and want to pick two, order not mattering, there are 4C2 = 6 ways to do that. Two of the physical quantities are defined in terms of the other two. (Current is change in charge over time. Voltage is change in flux over time.) That leaves four possible relationships: resistance, inductance, capacitance, and memristance. These are the values we use in every-day electronics design and analysis. (Well, not memristance, but one can dream.)
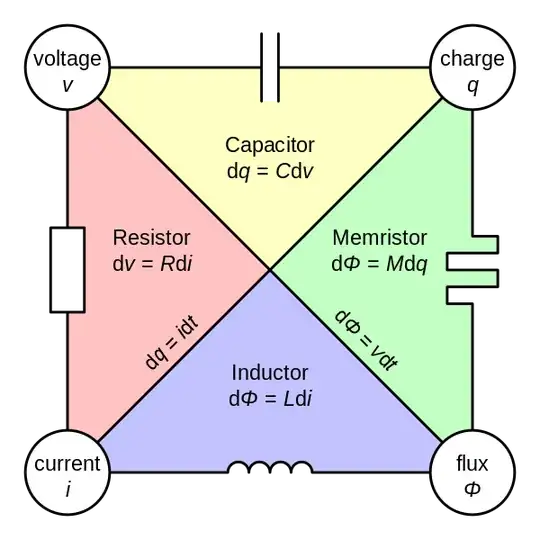
If you want another fundamental component, you need another physical quantity to relate to these four. And while there are many physical quantities one might measure, none seem so tightly coupled as these. I'd suppose this is because electricity and magnetism are two aspects of the same force. I'd further suppose that since electromagnetism is now understood to be part of the electroweak force, one might be able to posit some relationships between the weak nuclear interaction and our four quantities of voltage, current, charge, and flux.
I haven't the first clue how this would be physically manifested, especially given the relative weakness of the weak nuclear force at anything short of intranuclear distances. Perhaps in the presence of strong magnetic or electrical fields affecting the rates of radioactive decay? Or in precipitating or preventing nuclear fusion? I'd yet further suppose (I'm on a roll) that the field strengths required would be phenomenal, which is why they're not practical for everyday engineering.
But that's a lot of supposition. I am a mere engineer, and unqualified to comment intelligently on such things. Am I in the ballpark? Are there theoretical or demonstrable mathematical relationships between the weak nuclear interaction and charge, voltage, flux, and/or current which would correspond to my above suppositions? Or am I just looking for symmetry where none exists?