Imagine two locations with different amounts of gravity. I carry up a weight in low gravity, move it on this height over to the other place, and let it fall down there with higher gravity.
Wouldn't falling down release more energy than lifting up hast cost? If so, is it theoretically possible to generate such a transition between different levels of gravity near to each other?
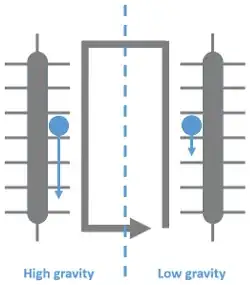
The main point is that Newtonian gravity fields are conservative. What that means is that it is impossible to have a configuration like the one you drew without there being gravitational fields pointing to the left and to the right in the regions where you want to do the 'horizontal' transfer.
For example, you might try to achieve this on Earth by taking the usual uniform gravitational field and locating a very heavy mass just under the foot of the conveyor belt on the left. This will mean, though, that as you move your mass from the foot of that conveyor belt you will be fighting against the attraction of that very same mass, as shown with the red arrows:
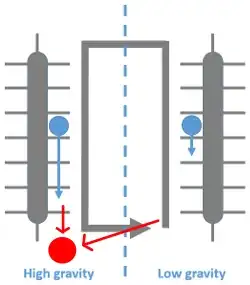
The net result is that doing both of those horizontal transfers takes work, and in fact it must take exactly the same amount of work as what you've gained from lifting the object in the weaker field. There are, of course, many possible ways to achieve the fields you want, apart from the one in my image, but because all gravitational fields are the sum of attractive forces to a bunch of point masses, and the field of each point mass is conservative, you will always, necessarily, have cross-pointing fields like the one I pictured that will do away with any perpetual motion engine.
