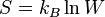Ice crystals are spatially ordered, and in every randomness there is a low possibility of temporarily order. If given enough boiling water, and sufficient time, could local clusters water molecules happen to be in a crystalized state?
This may seem absurd, but I believe it must be possible, imagine dropping an ice cube in boiling water(and water vapor) in a perfect closed system, the ice cube melts while the water keeps boiling (because of the water vapor), then because of Poincare recurrence theorem, there will be an similar ice cube after a sufficiently long but finite time.
EDIT: The temperature is 100 Celsius and 1 atm (not at triple point)