Pipe in a flowing river problem

Question

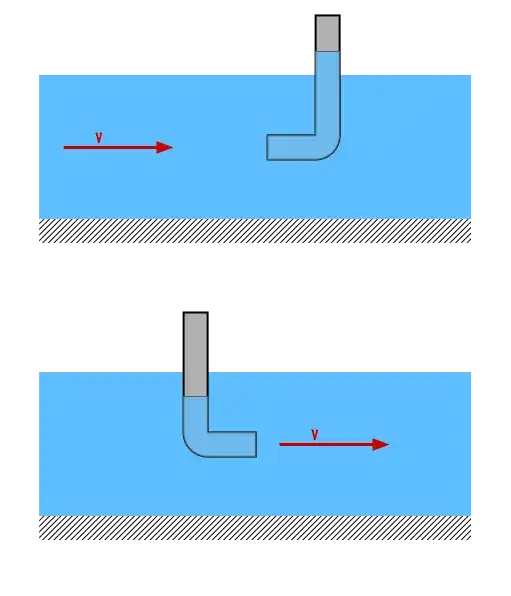
I'm working on a certain problem in fluid mechanics, which isn't really my strongest area. The problem is as follows: Curved pipe is partially submerged in a flowing river so that one end is pointing in the same direction as the velocity of river. Level of water inside of the pipe is 7cm higher than the level of river. Determine the speed of river.

Basically what I argued is that this reduces to Torricelli's law: level of water in pipe is constant so the velocity of the surface is zero (or very nearly so, I assume it would oscillate in real life), therefore water should move on the other end with $v_{2}=\sqrt{2gH}$, but it isn't since $v_{2}=v_{river}$ counteracts the movement.

I've tried to be more rigorous so I took pressures at the submerged end of pipe: $$p_{\text{water in pipe}}=p_{\text{atmosphere}}+\rho g h_{\text{depth}} + \rho g H_{\text{above water}}$$ $$p_{\text{river}}=p_{\text{atmosphere}}+\rho g h_{\text{depth}} + \frac{1}{2} \rho v^{2}$$

Since they have to be in equilibrium, pressures are equal and you get Torricelli's expression above.

Is my reasoning correct? It's somewhat counter-intuitive to me because the water is moving away from the pipe.

Answer 1

If you consider the following graphic:

The second one is your scenario, but let's consider the top one first. According to Bernoullis equation, $$ H=z+\frac{p}{\rho g}+\frac{v^2}{2g}=\mathrm{const}.$$ At the tube inlet: $H_\mathrm{left}=H_\mathrm {right}$, where $z$ is the geodesic height, $\frac{v^2}{2g}$ is the energy height, and $\frac{p}{\rho g}$ is the pressure height.

The geodesic height cancels out on both sides. But the energy height from the flow of the river presses against the tube inlet, which has to be balanced by raising the water level of the tube: $$ \frac{v^2}{2g}=\frac{p}{\rho g}=\Delta h $$ Thus $\Delta h$ is positive.

Now for the second scenario where the tube inlet faces in the direction of flow, the energy height is negative, because it "pulls" on the tube inlet, which consequently causes the water level in the tube to lower. $$ -\frac{v^2}{2g}=\frac{p}{\rho g}=\Delta h $$ Thus $\Delta h$ is negative.

I would conclude, that if the tube is pointing in the same direction as the velocity the water inside the pipe should actually be lower than the water surface.