11

One of the most useful black hole analogies I've seen imagines that space is "flowing" like a river into a black hole, and the point at which it flows in faster than c is the horizon. This analogy leads to the idea that a tachyon could escape from the "c"-based horizon and perhaps penetrate a bit further. Given that the tachyon has finite speed there would presumably be a horizon closer to the singularity that applies to the tachyon. However, could a tachyon device send us information about what's going on beyond the c-horizon?

Let's assume tachyons exist and we have a device that can generate an interpretable message transmitted w tachyons (the Apple iTach, if you will).

Brandon Enright
  • 12,030
Richardbernstein
  • 1,552

2 Answers2

9

For a particle moving faster than light (tachyon or not), indeed there is no horizon. For instance, particles can quantum-tunnel from below the horizon (it is known as "Hawking radiation"). Quantum tunneling is known to be possible with speeds exceeding the speed of light.

But this cannot be used to transfer information faster than light. As such, any particle which uses faster than lights speed to get out from below the horizon, will not carry any information, in other words, its spectrum will be statistically the same as of black body radiation, which is in agreement with the predictions for Hawking radiation.

Anixx
  • 11,524
1

Hawking radiation is more about the inward flow of negative energy (and outward flow of positive energy) caused by the action of the gravitational field.

As for black holes, there's a pretty simple way to check how tachyons react. Just looking at a conformal diagram :

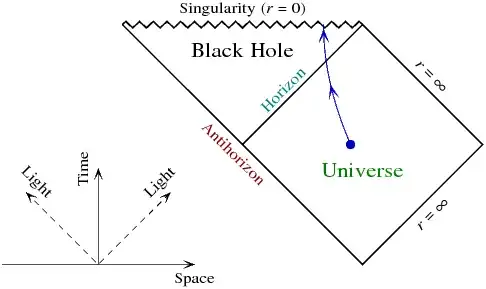
Conformal diagram of a black hole

(from this page for the source)

Conformal diagrams have the nice properties of identical causal properties with the original metric and that all light cones are at a 45° angle. Without breaking much of a sweat, you can see that even a casually spacelike curve would be able to get out of the event horizon.

Another way would be to look at the Kruskal coordinates

$ ds^2 = \frac{32M^3e^{r/2M}}{r} (-dT^2 + dX^2) + r^2 d\Omega^2 $

The horizon is at $T = \pm R$, the interior region at $T^2 - R^2 \in (0,1), T > 0$, the outside at $T^2 - R^2 < 0, R > 0$. A curve of the type

$T(\tau) = 1$

$R(\tau) = \tau$

will go from the singularity (or we can start a little way outside of it to avoid troubles) and go to infinity. Its tangent vector would be

$u_a = (0,1,0,0)$

and its curve will have the length

$l = \int_\varepsilon^\infty \sqrt{\frac{32M^3e^{r/2M}}{r}} dt$

which is obviously spacelike.

I'm not too sure how a free tachyon will fare, though I guess you just need to turn the Schwarzschild geodesic on its head and make it spacelike. But from the conformal diagram, my guess would be that a tachyon might actually have a hard time hitting the singularity.

Community
  • 1
Slereah
  • 17,006