Is speed of sound really constant?

Question

Does not speed of sound actually depend on the frequency and/or amplitude of the waves? If so, why it is constant?

Answer 1

The speed of sound is constant in the same sense that the mass of an object is constant.

In the typical audible range, at frequencies below, like, $100\:\mathrm{kHz}$ and sound pressures much less than atmospheric pressure, the behaviour of air is very well described by a simple linear wave equation that's purely second order in both space and time. As a result, the dispersion is linear ($|k| \propto \omega$), and phase or, equivalently, group velocity is constant.

Much the same in mechanics: whilst nothing moves anywhere near the speed of sound, momentum and speed are related linearly as described by Newton's laws of motion; we call the ratio mass and it's constant.

Not really though: special relativity tell us that when $v$ approaches the speed of light, you can push kinetic energy and thus momentum ever higher by accelerating an object, but it won't become faster to the same degree. One way to look at this is saying the mass increases.

Similarly, when you go to high frequencies, the wavelength shrinks to a range comparable to the material's internal structure. Therefore, you can't really use a differential equation anymore to describe the spatial component; the dispersion becomes more complicated and the speed of sound isn't constant anymore. Or, if the sound pressure is in a similar range as the air pressure, the behaviour becomes nonlinear alltogether, and you get shock-wave phenomena.

Answer 2

The speed of sound depends primarily on the properties of the medium: density (atomic weight), modulus (for solids), and adiabatic index (for gases). This means that it changes with composition of air (which is one reason why you sound funny when you speak after inhaling helium) and for a given gas, with temperature (see http://www.sengpielaudio.com/SpeedOfSoundPressure.pdf).

Mathematically, for small amplitude sound in gas the speed is given by

$$c=\sqrt{\frac{\kappa \;p_0}{\rho}}$$

Now the ratio $\frac{p_0}{\rho}$ (where $p_0$ is the pressure and $\rho$ the density) depends on temperature, but not on pressure. $\kappa=c_p/c_v$, the ratio of heat capacity at constant pressure and constant volume, respectively; $\kappa$ is constant for a given gas (it depends on whether it's mono-atomic or not: for atomic gases like He the ratio is $\frac53$, while for air it's $\frac75$)

All of this assumes small pressure variations - which holds true for most "ordinary" sounds. At SPL (sound pressure level) above 190 dB or so, the minimum pressure in the sound wave (the "trough") wants to go negative, and the pressure wave no longer behaves sinusoidally. At this point the simple math breaks down, and it's possible for very loud sounds to travel at a different speed.

Frequency doesn't really have anything to do with it - the ony way in which frequency is implicated in sound propagation is in attenuation: high frequency sounds are attenuated a little more strongly than lower frequency sounds.

Answer 3

The speed of sound is only very roughly a constant.

It depends on pressure (and so temperature/density), molecular weight of the gas and frequency

Answer 4

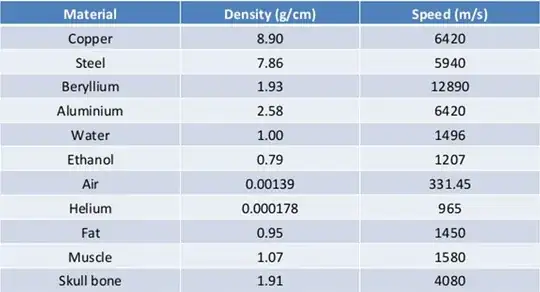The speed of sound depends on the medium in which it travels. In air it can be affected by ambient temp, relative humidity , as well as atmospheric pressure. The speed usual quoted at a standard temp and pressure.

http://byjus.com/physics/speed-of-sound-propagation/