Suppose a wheel with radius $R$ is resting on a non-inclined surface. A torque $\tau$ is applied to the wheel center. In an attempt to prevent wheel from spinning, the ground applies a static friction force to the wheel at the contact point (parallel to the surface), then the wheel starts rolling without spinning. The same friction force also acts as a torque on the wheel around its axis. This scenario is depicted below:
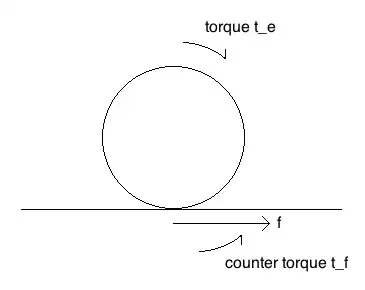
I'm trying to find the magnitude of the force the ground applies to the wheel - that is, the force which drives the wheel forward (which should be the same in magnitude as the force the wheel applies to the ground at the contact point).
That's how I'm doing it:
The relation between linear acceleration $a$ and angular acceleration $\alpha$ for a pure rolling movement is given by \begin{equation} \tag{1} a = \alpha \centerdot R, \end{equation}
The relation between torque $\tau$ and angular acceleration $\alpha$ is
\begin{equation} \tau = I \centerdot \alpha \end{equation}
where $I$ is the moment of inertia of the wheel around its axis.
The relation between torque $\tau$, force $f$ and lever arm $R$ is:
$$\tau = f \centerdot R$$
Being the engine torque $\tau_e$, the friction force $f$, the counter torque due to friction force $\tau_f$ and the moment of inertia of the wheel $I$ around its axis given by $\frac{1}{2}mR^2$:
The linear acceleration of the wheel is due to the friction force only:
$$f = ma$$ $$a = \frac{f}{m}$$
This is the counter torque the ground applies on the wheel's edge (negative, because it pointing in the opposite direction of $\tau_e$):
$$\tau_f = -f \centerdot R$$
The net torque causes angular acceleration on the wheel:
$$\tau = \tau_e + \tau_f$$ $$\tau = \tau_e - f \centerdot R$$ $$\tau = I \centerdot \alpha$$ $$\alpha = \frac{\tau}{I}$$ $$\alpha = \frac{\tau_e - f \centerdot R}{I}$$ $$\alpha = \frac{\tau_e - f \centerdot R}{\frac{1}{2}mR^2}$$
Substituting $\alpha$ and $a$ in $(1)$ gives:
$$\frac{f}{m} = \frac{\tau_e - f \centerdot R}{\frac{1}{2}mR^2}R$$
Rearranging:
$$f = \frac{2}{3}\frac{\tau_e}{R}$$
And that is the force $f$ from static friction which pulls the wheel forwards without making it spin or slip, and consequently, the force the wheel applies to the road surface at the contact point.
But I found this link: http://www.asawicki.info/Mirror/Car%20Physics%20for%20Games/Car%20Physics%20for%20Games.html
And it says: "The torque on the rear axle can be converted to a force of the wheel on the road surface by dividing by the wheel radius. (Force is torque divided by distance)."
That statement doesn't match the approach I used above. If the force of the wheel on the ground was simply engine torque divided by radius (negative, since it pointing in the opposing direction):
$$f = -\frac{\tau_e}{R}$$
then the counter torque applied to the wheel would be
$$\tau_f = -f \centerdot R$$
that implies that $\tau_f = -\tau_e$.
That means the net torque would be zero, and the wheel would just slip without rotating at all.
Am I doing something wrong on my calculations?