3

I'm trying to get my head around a problem (I should have checked whether I had the answer in class, the exams are coming up now and I don't know if I'll get a lecturer response over the holidays)

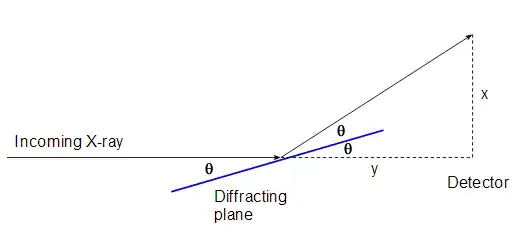
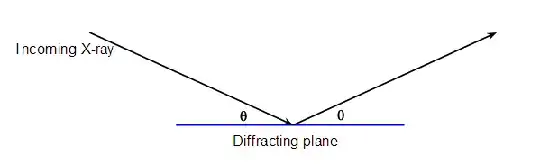
I can't get figure out the relationship between $\theta$ and $2\theta$ in the diagrams supposedly making clear how a crystal lattice diffracts.

From what I've read just now my understanding is that Bragg diffraction is actually transmission part-way into the crystal, then reflection off of an atom inside, hence the angle is twice the incident angle.

The textbook we've been referred to for further reading makes no note of a $2\theta$ (it can be read here).

The example used in the lecture is below

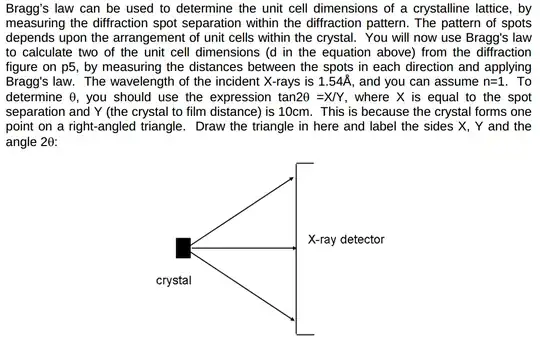
enter image description here

I obtained an answer by using a right-angled triangle made by the X-ray detector at the middle arrow, as this is the only perpendicular angle I can see. I really don't get how this would give the angle at the crystal as $2\theta$ (and I'm not at all confident that I should halve this angle to use in calculation of $\theta$

Can someone explain why I need to do so (as despite my misgivings, this is clearly indicated as the correct procedure). I've obtained an answer and am confident with the theory, maths etc., I just don't see the derivation of the $2\theta$ as opposed to $\theta$.

John Rennie
  • 367,598
Louis Maddox
  • 167

1 Answers1

6

Assuming I've understood your setup correctly this is where the $2\theta$ comes from:

A thousand words

Typically we think of the diffracton experiment with this geometry:

For the unelightened

But that means you have to rotate the X-ray source to change $\theta$ and this is usually inconvenient. In practice you keep the X-ray source constant and you rotate the diffracting plane by $\theta$ and the detector by $2\theta$.

In a powder pattern the diffracting planes are all simultaneously present and the line of the film appears at $2\theta$.

John Rennie
  • 367,598