1

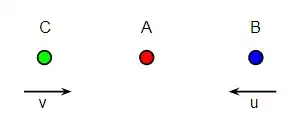
Suppose there are two observers $A$ & $B$ both are in motion, now $A$ sees $B$ is moving with speed $'u'$. A says that another object $'d'$ is moving with speed $c+u$ w.r.t. A in the same direction as $B$. What stops him from saying this ?

The formula $\frac {u+v}{1+\frac{uv}{c^2}}$ is such that $'v'$ is speed of the object $'d'$ w.r.t.$ B$ and not $A.$ and $u$ is the speed of $B$ w.r.t. $A$, now even though $B$ also sees that the object $'d'$ moves faster than the speed of light. He can still always see light to travel with the speed of light and also he can be an inertial observer?

What is the problem here?

Qmechanic
  • 220,844
Isomorphic
  • 1,616

2 Answers2

3

Let's start with what A sees:

SR1

As per your question we'll assume that $u + v > c$, though individually $u$ and $v$ must be less than $c$ because we can never observe speeds faster than light.

Now, you are correct to say that from the perspective of A the relative velocity of B and C is greater than light. But when we talk about $c$ being the fastest speed possible we mean the fastest speed relative to the observer i.e. in this case relative to A.

The next question is what B sees:

SR2

We know B will see A moving at the speed $u$, but the question is what speed will B see C moving? Will B see C moving at a speed, $w$, faster than light? The answer is no, because this is where the equation for combining relativistic speeds applies. The speed $w$ is given by the formula you quote:

$$ w = \frac {u+v}{1+\frac{uv}{c^2}} $$

and this speed is always less than $c$.

John Rennie
  • 367,598
2

The situation in which A observes some object moving at a velocity $c+u$ cannot occur within the framework of special relativity, therefore your scenario is meaningless. The theory puts an upper speed limit on observable motion, which cannot even be reached by massive bodies, but only massless ones. This limit is given precisely by $c$. Hence, assuming that $u$ is positive, nothing can move at $c+u$.

Frederic Brünner
  • 15,932