9

I was wondering if anyone can show me why some orbital resonances are unstable. For example in the asteroid belt there is a depleted distribution at 3:1 resonance with jupiter. What is the cause of this depletion and is it likely that other planets play an effect in determining the width of the depleted region or is it from some collisional process in the belt ( defined as full width half maximum of the depleted region)? A mathematical argument would be preferred but any ideas on the FWHM of the depletion would be appreciated.

enter image description here

Anode
  • 818

1 Answers1

8

Kepler's 3rd Law: The square of the orbital period of a planet is proportional to the cube of the semi-major axis of its orbit.

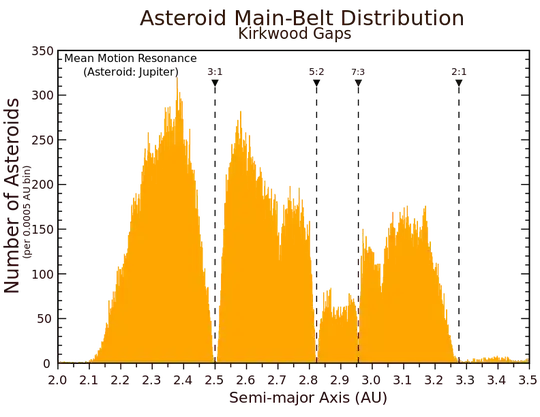
If we take Jupiter's semimajor axis of 5.2 AU (avg value), then objects at 2.5 AU, 2.82 AU, 2.95 AU, 3.25 AU have orbital periods shorter than Jupiter by a factor of 3:1, 5:2, 7/3 etc. The fact that the ratios for the deepest gaps involve the smallest integers is not coincidental.

The fundamental (pardon the pun) here is resonance. Essentially any object in resonance with Jupiter will gain so much energy from passing by it at such regular intervals that it cannot stay in that orbit (it will upgrade to a higher orbit). Basically it's a recurring gravitational slingshot maneuvre that naturally exists for any object residing in a Kirkwood gap orbit.

This is why orbits corresponding to periods of simple ratios with Jupiter's are almost completely vacated of objects. If you observe more closely you will find minor gaps: 2.71 AU for example. By my calculation, that gives an orbital period of 0.376 Jupiter's--thats 3:8, meaning an object at 2.71 AU orbits the sun 8 times in the time it takes Jupiter to do 3. But an object at 3.28 AU (2:1 resonance) gets pulled by Jupiter twice in the time it takes Jupiter to orbit, and this pulling is always in the same two locations.

Theoretically, the largest resonance occurs at 1:1 ratio, but this is more likely to happen as you push a child on a swing rather than a natural occurrence in astrophysics.

gregsan
  • 4,403