Is there any solution to the potential flow around a square cylinder?

Question

Potential flow around a circular cylinder is a classic solution. But I am wondering if there is any solution similar to this for the flow past a square cylinder?

Answer 1

Flow around a square cylinder

Similar solution to a cylinder but more violent von-karman vortex street because separation happens at an edge..

Notation of variables for a flow around a square cylinder The Reynolds number is defined as $Re = Ud/\nu$ and stands for a ratio between the inertial and viscous forces.

a) Re<55

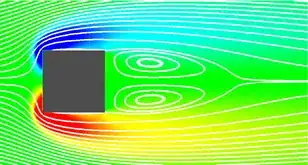
Re=30, alpha=0 Re=30, alpha=0 a) Re>55

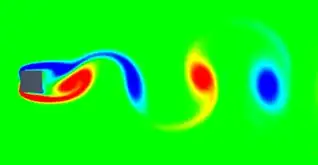
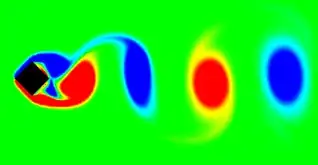
Karman vortex street: Re=30, alpha=0 Karman vortex street: Re=30, alpha=0

Answer 2

I am not an expert, but the thing I would do would be to use conformal invariance of potential flow. You would find a conformal transformation take a circle into a square, then take your potential function for the circular cylinder, and put this function through the conformal transformation. Derivatives give you the velocities for the square geometry.

I am not sure exactly what the conformal transformation is, but it won't be something you can do analytically because it involves elliptic integrals (I think). Also, the solution will probably have singularities at the corners of the square, judging by what other people are saying. Therefore the solution found this way won't be physically realizable.

Answer 3

The flow around a square is dominated entirely by viscous effects and the vortex shedding due to the boundary layer. Additionally, at very high Reynolds numbers such that viscous effects are minimal, the square has considerable separation which cannot be solved with the potential equations.

Because potential flow requires both irrotational and inviscid assumptions, I do not think that it can be used for the flow around a square cylinder. It works well for circular cylinders only at low enough Reynolds numbers that the flow does not separate around the cylinder. But for the square, that doesn't hold.