Converting between Galactic and Ecliptic coordinates

Question

I was hoping someone would be able to tell me the formula to convert between ecliptic and galactic coordinates. I've been able to convert values using http://lambda.gsfc.nasa.gov/toolbox/tb_coordconv.cfm but have no idea how they were able to calculate that. Thanks in advance :)

Answer 1

Both ecliptic and galactic coordinates are spherical coordinate systems that involve measuring angles on the celestial sphere. There are two equivalent ways to convert between such two coordinate systems:

1. A transformation by deriving a general rotation matrix, for example using Euler angles;
2. Finding an appropriate spherical triangle and calculating its sides and angles using Spherical trigonometry.

Let's take a closer look at the second method. A spherical triangle is a triangle on a unit sphere (in our case the celestial sphere) that is formed by the intersection of three great circles.

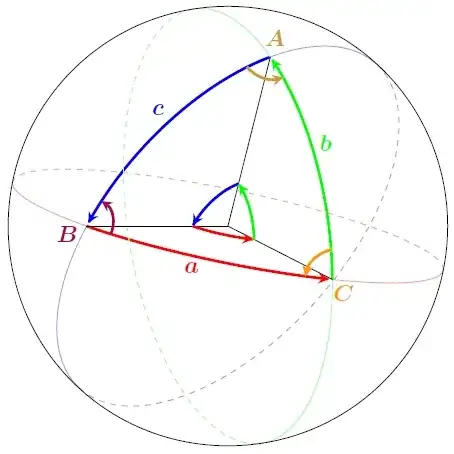
It has three 'angles' ($A$, $B$, and $C$) as well as three 'sides' (the arc lengths $a$, $b$, and $c$). Note that the sides are in fact also angles. There exist several useful relations between these 6 elements: the most fundamental are the cosine rules: $$ \begin{align} \cos a &= \cos b\, \cos c + \sin b\, \sin c\, \cos A,\\ \cos b &= \cos c\, \cos a + \sin c\, \sin a\, \cos B,\\ \cos c &= \cos a\, \cos b + \sin a\, \sin b\, \cos C. \end{align} $$ From these, one can also derive the sine rules: $$ \frac{\sin A}{\sin a} = \frac{\sin B}{\sin b} = \frac{\sin C}{\sin c}, $$ and the sine-cosine rules: $$ \begin{align} \sin a\, \cos B &= \cos b\, \sin c - \sin b\, \cos c\, \cos A,\\ \sin b\, \cos C &= \cos c\, \sin a - \sin c\, \cos a\, \cos B,\\ \sin c\, \cos A &= \cos a\, \sin b - \sin a\, \cos b\, \cos C. \end{align} $$ Now we can use these identities to convert between two spherical coordinate system. Consider the following figure:

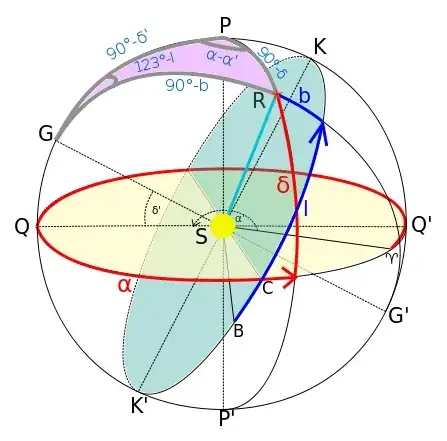
This figure shows the transformation from equatorial to galactic coordinates, but the transformation from ecliptic to galactic coordinates is analogous. $P$ is the equatorial pole, $\gamma$ is the vernal point, $G$ is the galactic pole and $B$ is the galactic centre. The galactic plane and the equatorial plane intersect at the line $SC$, and $K$ is the intersection of the galactic plane with the great circle through $G$ and $P$. A celestial object, located at $R$, has equatorial coordinates $(\alpha,\delta)$ and galactic coordinates $(l,b)$. Also, the galactic pole has equatorial coordinates $(\alpha_G,\delta_G)$ (in the figure, these are called $(\alpha',\delta')$ and the galactic centre has equatorial coordinates $(\alpha_B,\delta_B)$ (not shown in the figure). In the epoch J2000 (see wikipedia), $$ \begin{align} \alpha_G &= 12^\text{h}\,51^\text{m}.4 = 192^\circ.85,&\qquad \delta_G &= +27^\circ.13,\\ \alpha_B &= 17^\text{h}\,45^\text{m}.6 = 266^\circ.40,&\qquad \delta_B &= - 28^\circ.94. \end{align} $$

In order to convert between equatorial and galactic coordinates, one now has to solve the pink spherical triangle $PGR$. It is straightforward to see that the three sides are $90^\circ - \delta_G$, $90^\circ - b$, and $90^\circ - \delta$. The angle between $PG$ and $PR$ is $\alpha-\alpha_G$. Finally, in order to find the angle between $PG$ and $GR$ we have to solve another spherical triangle, namely $PKB$: the arc length $PB$ is $90^\circ - \delta_B$, the arc length $PK$ is $\delta_G$ (since the arc length $GK$ is $90^\circ$), and the angle between $PB$ and $PK$ is $\alpha_K-\alpha_B$, with $\alpha_K=\alpha_G+180^\circ$. Therefore, applying the cosine rule in $PKB$, we find $$ \begin{align} \cos(BK) &= \sin\delta_B\,\cos\delta_G - \cos\delta_B\,\sin\delta_G\,\cos(\alpha_G-\alpha_B),\\ &= -0.4307 -0.1130 = -0.5437, \end{align} $$ so that the angle $BK$ is equal to $122^\circ.9$. Therefore, the angle between $PG$ and $GR$ is $122^\circ.9-l$. Now we can apply the cosine and sine rules in the triangle $PGR$, to convert equatorial coordinates to galactic coordinates. We get $$ \begin{align} \sin b &= \sin\delta_G\,\sin\delta + \cos\delta_G\,\cos\delta\,\cos(\alpha-\alpha_G),\\ \cos b\,\sin(122^\circ.9-l) &= \cos\delta\,\sin(\alpha-\alpha_G),\\ \cos b\,\cos(122^\circ.9-l) &= \cos\delta_G\,\sin\delta - \sin\delta_G\,\cos\delta\,\cos(\alpha-\alpha_G). \end{align} $$ (the first eq. is the cosine rule applied to $GR$, the second is the sine rule between $GR$ and $PR$, and the third is the sine-cosine rule for $GR$). These three equations can be solved to get $(b,l)$. Conversely, from galactic to equatorial coordinates: $$ \begin{align} \sin\delta &= \sin\delta_G\,\sin b + \cos\delta_G\,\cos b\,\cos(122^\circ.9-l),\\ \cos\delta\,\sin(\alpha-\alpha_G) &= \cos b\,\sin(122^\circ.9-l),\\ \cos\delta\,\cos(\alpha-\alpha_G) &= \cos\delta_G\,\sin b - \sin\delta_G\,\cos b\,\cos(122^\circ.9-l). \end{align} $$ The conversion between ecliptic and galactic coordinates is completely analogous, with equatorial coordinates $(\alpha,\delta)$ replaced with ecliptic coordinates $(\lambda,\beta)$, and $$ \begin{align} \lambda_G &= 180^\circ.01,&\qquad \beta_G &= +29^\circ.80,\\ \lambda_B &= 266^\circ.84,&\qquad \beta_B &= - 5^\circ.54. \end{align} $$ We find $$ \begin{align} \cos(BK) &= \sin\beta_B\,\cos\beta_G - \cos\beta_B\,\sin\beta_G\,\cos(\lambda_G-\lambda_B),\\ &= -0.1119, \end{align} $$ so that the angle $BK$ is $96^\circ.43$. Finally, $$ \begin{align} \sin b &= \sin\beta_G\,\sin\beta + \cos\beta_G\,\cos\beta\,\cos(\lambda-\lambda_G),\\ \cos b\,\sin(96^\circ.43-l) &= \cos\beta\,\sin(\lambda-\lambda_G),\\ \cos b\,\cos(96^\circ.43-l) &= \cos\beta_G\,\sin\beta - \sin\beta_G\,\cos\beta\,\cos(\lambda-\lambda_G), \end{align} $$ and conversely $$ \begin{align} \sin\beta &= \sin\beta_G\,\sin b + \cos\beta_G\,\cos b\,\cos(96^\circ.43-l),\\ \cos\beta\,\sin(\lambda-\lambda_G) &= \cos b\,\sin(96^\circ.43-l),\\ \cos\beta\,\cos(\lambda-\lambda_G) &= \cos\beta_G\,\sin b - \sin\beta_G\,\cos b\,\cos(96^\circ.43-l). \end{align} $$

Answer 2

Perhaps you're looking for something you can just punch into a spreadsheet instead of a generic matrix transformation? I've found it's easier to go from equatorial to other systems. So you can move it from ecliptic to equatorial (in degrees):

$\alpha=tan^{-1}(\frac{sin(\lambda) *cos(\epsilon)-tan(\beta)*sin(\epsilon)}{cos(\lambda)})$

$\delta=sin^{-1}(sin(\beta)*cos(\epsilon)+cos(\beta)*sin(\epsilon)*sin(\lambda))$

Where $\epsilon$ is the obliquity of the ecliptic based on your reference epoch.

Then equatorial to galactic:

$b=sin^{-1}(cos(\delta)*cos(27.4)*cos(\alpha-192.25)+sin(\delta)*sin(27.4))$

$l=tan^{-1}(\frac{sin(\delta)-sin(b)*sin(27.4)}{cos(\delta)*cos(27.4)*sin(\alpha-192.25)})+33$

The numbers for the formula come from how the galactic is setup where $\alpha=192.25$ for the north pole and $\delta=27.4$ for the ascending node of the galactic plane where the equator $l=33$

NOTE: Whenever you compute the inverse tangent you have to remove the ambiguity based on the quadrant. For example $tan^{-1}=\frac{y}{x}$ The angle is between 0-90 if both x & y are positive. The angle is between 90-180 if y is positive and x is negative. The angle is 180-270 if both x and y are negative. The angle is between 270 and 360 if y is negative and x is positive. Just add or subtract 180 or 360 to put the result in the correct quadrant.