I took this picture of a water feature on campus at Caltech: 
The lamps at the bottom of this pool have large, circular shadows surrounding them, but there are also bright rings of light surrounding those shadows. Since there are no obstructions in the water to block the light, why are these round shadows being formed?
The Short Answer: Total Internal Reflection. These circular shadows are formed by the rings of reflected light bouncing off the water's surface and illuminating the bottom of the pool.
The Long Answer:
Since the lamps are embedded in the bottom of the pool, they emit light only upwards. Therefore, there is no need for an obstruction to cause a shadow: they just don't shine on the bottom of the pool. In fact, if the pool were drained, the bottom of the (now dry) pool would be entirely dark because all the light would escape upwards into the night sky. So the real question is not "Why are there shadows?" but rather "Why are there rings of light surrounding those shadows?".
The rings of light form due to reflections off the surface of the water bouncing back down towards the bottom of the pool. When light passes from one medium (like water) into another (like air), it bends in a process called refraction following a rule known as Snell's Law. However, not all of the light escapes the first medium; some of the light reflects off the boundary between the media (usually following the so-called "law of reflection").
However, when light travels from a denser medium (i.e. water) into a less dense medium (i.e. air), the overwhelming majority of the light will be transmitted (and very little will be reflected) so long as the light hits the boundary at an angle sufficiently close to perpendicular. However, beyond a special angle called the critical angle, the vast majority of the light will be reflected in a process known as "total internal reflection" which prevents the light from escaping into the air.
In this case, the large, round shadow is caused by a ring of reflected light bouncing off the bottom of the water's surface and illuminating the bottom of the pool.
As an interesting side note: The diameter of the circular shadow can be used to experimentally determine the index of refraction of the water using the following diagram:
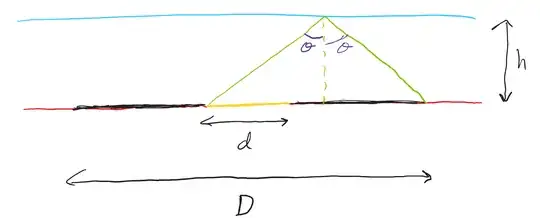
where $d$ is the diameter of the light, $D$ is the diameter of the shadow, $h$ is the depth of the water, and $\theta$ is the critical angle.
Assuming the index of refraction of air to be approximately $1$ (i.e. indistinguishable from a vacuum), then a little bit of trigonometry results in the following formula for the index of refraction of the water: $n=\sqrt{1+(\frac{4h}{D+d})^2}$.
I've measured this pool and know that the water has a depth of around $h=10.125 \text{ in.}$, the lamps are about $d=3 \text{ in.}$ across, and the little tiles on the bottom of the pool are about $2 \text{ in.}$ on a side (which implies that the shadows in this picture are approximately $D=46 \text{ in.}$ wide). This gives us an experimental index of refraction of water of $n=1.297$. This number agrees to two significant figures with the standard, accepted index of refraction for water. Not bad!
As a final comment: Some careful thought will also show that $D+d$ must be a constant of the system, so a point source of light would have a shadow of diameter $D+d$ ($49 \text{ in.}$) while a giant lamp of diameter $\frac{D+d}{2}$ ($24.5 \text{ in.}$) would have no shadow at all.