Could Faraday-Lenz law be understood from forces rather than from flux?

Question

Picture a magnet passing through an spiral wire. Because of Faraday-Lenz law we know that the change of flux on the spiral wire will create eddy currents inside of it (this currents will create a magnetic field that goes against the increasing magnetic field of the magnet entering the wire). All of this is given the following Maxwell equation: $$ \oint\mathbf E \cdot d\mathbf r = -\frac{d}{dt}\iint\mathbf B \cdot d\mathbf S $$

But always there has been something that bothered me: flux. Flux seems useful in mathematical terms, but seems almost of no physical meaning, yet they appear in Faraday-Lenz law to explain this kind of phenomena.

Forces, on the other hand, seem more tangible and with a more mundane meaning and interpretation (leaving QFT apart).

My question is, could this law be understood from a force interpretation perspective?

For example, imagine the magnet as said before. The spiral is located on the $yz$ plane. The magnet is moving on the $x$ direction.

If we interpret the result like this: $$ \mathbf F = e \mathbf v \times \mathbf B $$ This is the force exerted by the magnet on the wire. It can be easily seen that the force goes on the direction eddy currents will follow obeying Faraday-Lenz law. So far so good. Now we know that by the definition of electric field: $$ \mathbf E = \frac{\mathbf F}{e} \\ \; \\ $$ But: $$ \mathbf F = e \mathbf v \times \mathbf B $$ Hence: $$ \mathbf E = \mathbf v \times \mathbf B $$ By Ohm's Law inside the wire: $$ \mathbf J = \sigma \mathbf E = \sigma \mathbf v \times \mathbf B $$ Finally we conclude that we have a current on the direction eddy will arise with the "flux interpretation". Now, analyzing some situations in case we are wrong:

For example, when the magnet is halfway through the wire the flux is maximum, hence $$ \frac{d}{dt}\iint\mathbf B \cdot d\mathbf S = 0 $$ and we arrive to the conclusion that the eddy currents will be zero: $$ \oint\mathbf E \cdot d\mathbf r = -\frac{d}{dt}\iint\mathbf B \cdot d\mathbf S = 0 $$ Now using the "force interpretation", when the magnet is halfway through the wire the $\mathbf v$ and $\mathbf B$ vectors are parallel, hence it's cross product is zero leaving, also, to no eddy currents.

This make sense, but I'm not completly sure if this derivation is right. The are also some flaws like, how the magnetic field created by the wire will influence the one created by the magnet itself, etc.

Can someone give me an insightful explanation and how Maxwell's equiations and Physical Models deal with this? I suspect relativity (as well as tensor calculus and differential geometry) has to do with this.

EDIT: (1) I do not want to replace the idea of flux, because it has been proven to be useful and fundamental on the description of EM. I just want to complement the interpretation of flux with forces because, for example, at microscopic level there exists carrier particle which mediate this forces, hence the idea of flux seems "disconnected" from reality or fundamental physics. (2) The sign on the Lorentz Force formula comes from thinking that the positive charges are the ones moving, rather than electrons.

Answer 1

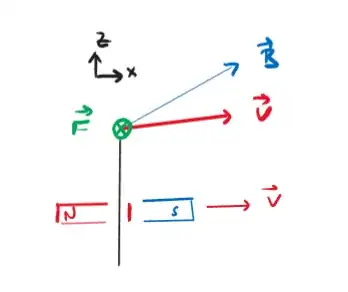
My question is, could this law be understood from a force interpretation perspective?

Half-yes. A kind of force, electromotive force, can be used to express and understand Faraday's law, and this is how Maxwell formulated it (and also what we mean today by Faraday's law as opposed to the Maxwell-Faraday equation). But even then, Faraday's law is still about the fact this electromotive force is given by the rate of change of magnetic flux.

Let us see how force comes into this.

Originally, Faraday formulated his law close to this: when the number of magnetic field lines going through a circuit changes, this induces electric current in the circuit, proportional to rate of that change.

Maxwell expressed this in terms of electric and magnetic field components, and a particular concept of force - the electromotive force (EMF), with the understanding that electric current is proportional to it. His formulation was close to this:

When magnetic flux through a circuit changes in time, there is "induced EMF" acting on the electric current in it as well, and this induced EMF is proportional to rate of change of that magnetic flux.

So, Maxwell formalized Faraday's description - instead of mentioning the induced current, he introduced induced EMF, which is a description of the effect of the force in a closed path - but magnetic field lines or magnetic flux still play central role in Maxwell's account of Faraday's law.

Faraday's law can't really be stripped of the notion of magnetic flux (or some equivalent notion such as the number of magnetic field lines). If someone does it and replaces it with e.g. changing distant electric currents in the past, then they may end up with some part of an alternative formulation of EM theory, but it would not be appropriate to call it Faraday's law.

What is EMF (for a closed path) in general? For any particular force (say, $k$-th force) acting on mobile charged particles, we can calculate the following line integral over closed path of the circuit $\gamma$, at a single time:

$$ EMF_k(t) := \oint_\gamma \mathbf f_k(\mathbf x,t) \cdot d\mathbf x. $$ This is the EMF for a closed path, associated with that $k-$th force.

It turns out (I'm not sure if Maxwell himself knew this, but I think it's likely) that Maxwell's induced EMF in a circuit made of thin wire can be understood as line integral of the following expression (it has dimensions of force per unit charge):

$$ \mathbf f = \mathbf E + \mathbf w\times \mathbf B, $$ where $\mathbf w$ is velocity of the wire or the conductor body element; it is not the velocity of the mobile charged particles unless electric current is zero.

Here people get confused, because the formula looks like the Lorentz force formula for force on a charged particle, and they think, see, the induced EMF is just due to the effect of the Lorentz forces of the magnet on the charged particles in the wire. But $\mathbf w$ is velocity of the wire, not velocity of the charged particles $\mathbf v_a$ in the wire, which may be different when current flows. So the formula is not a trivial sum of Lorentz forces by the magnet. It is deceiving to say the whole process is just due to the Lorentz forces by the magnet acting on the mobile charge. There are other forces by the wire as well, constraint forces which keep the charge inside the wire, which are important. This is better seen in the frame of the magnet, where the magnet is still and the wire moves; there, magnetic field is static, and the electric field vanishes. There is non-zero induced EMF (so-called motional EMF) also in this frame, and it is correctly given by the line integral of the magnetic term $\mathbf w\times\mathbf B$. However, this force at any element of the wire is not simply a sum of magnetic Lorentz forces by the magnet. This force does work on the mobile charge and transfers energy to them/from them, something magnetic Lorentz forces can't do.

To bring all of that together, Maxwell's induced EMF in a closed circuit, which may be still or moving, can be expressed as

$$ EMF = \oint_\gamma (\mathbf E + \mathbf w\times \mathbf B) \cdot d\mathbf x. $$ where $\mathbf w$ is velocity of the wire(conductor) element $d\mathbf x$.

If we interpret the result like this: $$ \mathbf F = e \mathbf v \times \mathbf B $$ This is the force exerted by the magnet on the wire.

You mean the force on a mobile charge in the wire (the force on the wire is different and not really connected to Faraday's law). This can be correct for an electron, if $e$ is positive number. A much better way to write it is

$$ \mathbf F = - q \mathbf v \times \mathbf B, $$ where $q$ is charge of the mobile charged particle. If $q = -e$ as in the case of an electron, then we get your formula.

I'm curious how you got to this formula. It's not clear this is the exact formula for the force, but there is an argument that it is at least approximately correct (for non-relativistic velocities), which follows.

The integral formula for EMF which I gave above suggests(not proves) there is an actual force on the mobile charge $e$ equal to:

$$ \mathbf F = q \mathbf E + q\mathbf w \times \mathbf B, $$ where $\mathbf w$ is velocity of the wire. Since it is zero in the example (the wire is still, so $\mathbf w = 0$), the magnetic term drops out and we have just

$$ \mathbf F = q \mathbf E. $$ where $\mathbf E$ is electric field of the moving magnet.

It turns out that electric field of a moving magnet, assuming the magnet is not charged, can be expressed (at least approximately), as

$$ \mathbf E = -\mathbf v \times \mathbf B \tag{*}. $$

This can be seen from the following argument. Approximately, magnetic field is the same in both frames, and in the frame of the magnet, the wire moves with velocity $-\mathbf v$. So in the frame of the magnet, any test charged particle moving with the wire has to experience magnetic Lorentz force $-q\mathbf v\times \mathbf B$. Since force on this test charge is approximately the same in both frames, force of approximately the same magnitude acting on the test charge is present also in the frame of the wire. But in this frame, since the test charge does not move, it can be only due to electric field whose vector is $\mathbf E = -\mathbf v\times \mathbf B$.

This whole argument could be made more precise by doing exact Lorentz transformation of the magnet EM field between both frames. I'm not sure if the formula (*) turns out to be exactly correct, or just an approximation.

With this or some other correct justification for the fact electric field of a moving magnet is given by the above formula (*), your explanation of the induced EMF action on current as due to force by the magnet acting on mobile charge in the wire is correct and standard. The force turns out to be the electric force due to electric field of the magnet.

Induced EMF in general is really due to all EM and constraint forces (by the wire, preventing the charge from jumping out of the conductor), acting on the mobile charge in the wire.

Answer 2

No, you cannot.

Consider just one loop of wire that you put a voltmeter and/or ammeter in it. Let this loop of wire be threaded through a toroidal choke such that no B field is actually on any part of this loop of wire, since an ideal toroidal choke can be made so that all the B field is kept inside the toroidal choke.

Since there is no B field on the loop of wire, by your Lorentz force law $\vec F=q(\vec E+\vec v\times\vec B)$, the lack of the B field implies that there is no magnetic contribution to the charges on the wire, and instead all of the forces pushing the charges in the wire to move, will be coming from the E field, and this E field only exists because the magnetic field that is totally confined in the toroidal choke, is changing.

Your scheme is thus doomed.

---

There are actually many textbook derivations of phenomena that can be successfully converted into forces on charges, and often the textbook derivations are complicated whereas the forces on charges view is much simpler. This just happens to be one of those that cannot be converted this way.

Note 1: The Lorentz force law never had a part that has the time derivative of magnetic field in it. There was never any chance for your scheme to work in the first place.

Note 2: Although standard introductory presentations always start from basic phenomena like Coulomb's law to "derive" Maxwell's equations, one should always note that the correct step, often missing from curriculum because of class time constraints, is that one needs to restart from Maxwell's equations and derive everything from there, including Coulomb's law. Maxwell's equations are the minimum assumptions from which you define what those EM fields are, and without them, you cannot even assert to know what your EM fields are. There is thus, yet again, no way to define your forces if you abandon Faraday-Lenz law.

Answer 3

I believe that what is missing in your analysis is the role of the induced electric field.

A changing magnetic field is accompanied by an associated electric field as per the local form of Faraday's equation. So, your $\vec{F}$ is not only $q \vec{v} \times \vec{B}$, but you need to consider $q \vec{E}$, where $\vec{E}$ is the induced electric field. We can remove the complication of the moving magnet by producing the variable magnetic field by means of a variable current in a coil. Let's consider a toroidal coil, with or without a magnetic material core (but let's avoid saturation to avoid complications). A sinusoidal current will produce a sinusoidally varying $\vec{B}$ field confined inside the core. No appreciable B field outside the solenoid. But there will be a significant induced electric field.

Source: Wikipedia

That field can be expressed in term of the time derivative of the magnetic vector potential $\vec{A}$ (plus a sign change) and its line integral will be the induced voltage along a path in the space around the coil. If you pick a closed path, its circulation is the EMF associated with that loop.

A charge in space - to my knowledge - will respond to the force $\vec{F} = q \vec{E}$, where E is the induced electric field.

When you put a non-perfect conducting loop around the solenoidal coil, there will be an interaction with the material, a redistribution of surface charge on it and the resultant electric field will be the superposition of the induced electric field (associated with the variable magnetic field in the core), and the coulombian electric field generated by the rearrange charge.

This of course instant after instant. I am assuming that the field are varying slowly enough to prevent radiation (quasistatics) and I am also neglecting the effect of the magnetic field generated by the current flowing in the secondary loop (no 'loading' of the primary coil).

Answer 4

While there isn't a perfect way to understand Lenz's and/or Faraday's law through forces, one could instead intuit a kind of force from the interactions between the $E$ and $B$ fields as described by the Maxwell-Faraday equation, particularly in its differential form: $$\nabla \times \mathbf E = -\frac{\partial \mathbf B}{\partial t} ,$$ which manages to describe the fields' interactions without needing to know the area. However, most of the work goes into interpreting the physics, which will deal with the area (and therefore flux) at some point in the problem.

In short, there is no direct force-based interpretation, and any such method would require unnecessary complications. For the most part, any E+M is best though of through fields instead of forces.