Free fall confusion

Question

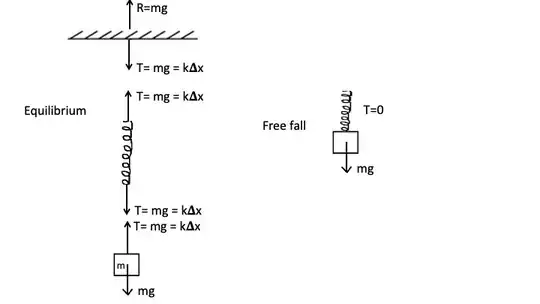
Here are 2 questions that many of us have not found a good answer too, even teachers avoid a perfect answer. I also somehow intuitively understand it, but how to explain this best?

1. A rock is hung to a spring balance. The spring balance reads some value > 0. Why will it be zero when both are allowed to fall? Who said that the rock is not still pulling down the spring (it appears like it still pulls)?

2. Why a particle in upwards accelerating elevator is experiencing a compressive force even if it is in the same state as someone falling freely?

Please realise, this is not HW questions. I posted this because they are in my white list: After so many days I couldn't perfectly explain them. Moreover this will help many a freshman.

Answer 1

1. A rock is hung to a spring balance. The spring balance reads some value > 0. Why will it be zero when both are allowed to fall? Who said that the rock is not still pulling down the spring (it appears like it still pulls)?

When the spring scale is held, say by you, the scale reads $\gt 0$ because the length of the spring increases until the spring restoring force ($k\Delta x$) equals the weight of the rock ($mg$) for a net force on the rock of zero. It is the increase in the length of the spring $\Delta x$ that results in a scale reading $\gt 0$. See the free body diagrams of the spring and rock below.

The combination of the spring and rock is in equilibrium (not accelerating) due to the sum of the external forces (your upward force $R$ in the diagram at the left, and the downward force of gravity acting on the rock, $mg$) being zero. If you release the scale $R$ becomes $0$ and the spring and rock go into free fall (figure to the right) as there is no longer an upward force supporting the rock and spring and therefore no longer tension in the spring. The spring returns to its unstretched length and the scale reads zero.

You can verify the behavior of the spring with a simple experiment. If you don't have a spring scale, you can use a rubber band. Although the rubber band doesn't strictly obey Hooke's law (its force displacement curve is non linear) the principle is the same as a spring. Hold the rubber band at one end and suspend a weight sufficient to stretch the rubber band, just like the spring in the spring scale will stretch and indicate the amount of weight. Now release the rubber band. You will observe that the rubber band immediately snaps back to its original length as it free falls with the weight.

2. Why a particle in upwards accelerating elevator is experiencing a compressive force even if it is in the same state as someone falling freely?

The state of the particle is not clear in your question. But it seems like you're describing a particle resting on the floor of an upward accelerating elevator. If that's the case, then I'm not sure why you would say it would behave the "same as someone falling freely". Perhaps you could clarify this.

Hope this helps.

Answer 2

To both of your questions, the answer is that gravity accelerates all objects at the same rate ($9.81 m/s^2$ at the earth's surface). That's known as the weak equivalence principle (WEP).

To my mind, the best way to see this has to be true is to consider 2 objects of different masses, both falling under the influence of gravity. If WEP were wrong, one of them - presumably the one with less mass - will accelerate slower than the other. Now tie them together with a string, and you can then look at the combined object in 2 ways.

1. The lighter one, being slower, will hold back the heavier one. Hence the combined speed will be somewhere between the two individual speeds.
2. As they are tied together, they form one object, which is heavier than either one. Hence its acceleration will be greater than either of the two.

This is an obvious contradiction that is only resolved if they both have the same acceleration. It is Galileo who first thought of this. That it is true is confirmed to great accuracy by many experiments. In addition, Prof. Brian Cox demonstrated it in a huge NASA vacuum chamber and, of course, Apollo 15 showed it on the moon.

Once you accept that, your rock and spring balance will move perfectly in unison. On the other hand, your particle in the elevator is not falling freely, so it cannot be expected to behave in the same way as an object in free fall.

Answer 3

The spring balance only shows a value >0 if it is fixed/supported at the top. Whatever supports the spring, does in this case carry the weight of the rock. If you disconnect the spring, there is nothing to support anymore and the weight shows as 0.

Similarly for the upward accelerating elevator. You only have a compression force as long as the floor supports you. If you jump upwards in upward accelerating elevator, you will be weightless as long as you are not connected to the floor.

Answer 4

True. The spring even after being left to fall and still connected to the rock has some extension ∆x in it.(The instant just after cutting the connection point between the spring and wall to which it is hanged.)(I am placing my insight .In real world scenerio and not considering the ideal cases of the mass of spring to be zero) but now there is no upward tension due to the wall. So instantaneously the tension changes from MG to zero. But still there is some extension in the spring. So it will exert a force for small period of time on the block. Till its extension becomes zero and it will because there is no tension opposing the tendency of the spring to remain at its natural length. In fact the spring exerts force due to the tendency or springiness. Thus the acceleration of the block spring system will be g. But also consider simple harmonic motion of the spring the spring will attain some kinetic energy when trying to reach its natural length so this spring from the time of breaking till the time it reaches it's natural length is pulling the block by some small force but now it will also get compressed due to its kinetic energy increment. Thus the spring will go into simple harmonic motion which is damped of course in real life scenario. And the force acting on the block will be less than mg and after a few instance more than mg but the net acceleration of the spring block system will remain g.