Why is the direction of angular velocity or angular momentum perpendicular to the plane where the circular motion actually occurs?

Question

I always thought that it was just a mathematical thing (as we can't use something like a curvy vector) and has no real life physical significance. However, i saw the working of a gyroscope which according to me clearly uses the direction of these angular quantities being perpendicular to the plane and thus the underlying phenomenon is explained. I don't understand why is has the direction perpendicular to the plane? Is it just not a mathematical convention?

Answer 1

Indeed, it is just a mathematical convention to associate a perpendicular vector direction with an angular proporty and to choose that vector direction to match the spinning direction according to the right-hand rule. There is no physical "thing" that sticks perpendicularly out from a spinning bicycle wheel when considering angular velocity i.e., it is purely a mathematical concept.

But by keeping such mathematical conventions consistent, we can get physical results through mathematical operations on such (pseudo) vector quantities. For example, add two angular velocity vectors, and the result is zero if their spinning is opposite, since that would be converted to two opposite but equal (pseudo) vector quantities. Do a dot product on them, and if it is zero, then the to Mike wheels are positioned at a right angle to each other.

When physics becomes complicated, then working through the mathematical operations on such fixed mathematical conventions can allow us to still arrive at a physical result. That might be what you see e.g. in work on gyroscopes, which arguably is one of the more advanced topics from classical mechanics.

Answer 2

You are trying to understand the geometry of rotations.

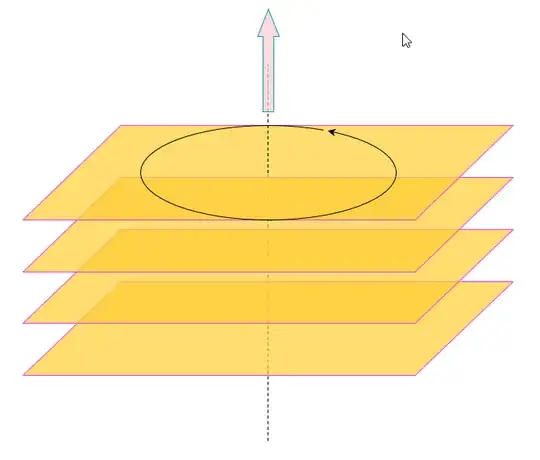
1. All rotations happen in a plane.

   

   This means that each particle on a body stays on a plane, and at a fixed distance from the rotation axis.

   The rotation axis is the locus of points that do not move under a pure rotation. Every other point orbits around the axis of rotation, each on its own plane that is perpendicular to the axis.

2. To describe a plane, you need the vector that is orthogonal to the plane and its distance from the origin. Since all the planes of rotations have a common orthogonal vector, we use this vector to describe the rotation. This is the rotational velocity vector $\vec{\omega}$. The magnitude of the vector describes the speed of rotation such that the linear velocity of any point located at $\vec{r}$ relative to the rotation axis is $$ \vec{v} = \vec{\omega} \times \vec{r}$$

3. Combine all the centers of rotation for each plane to describe the axis of rotation which is a line in 3D space.