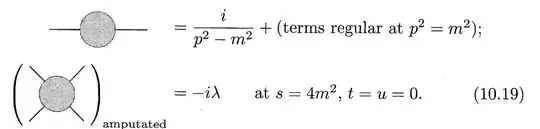Why can we shift the renormalization scale in the RG flow?

Question

It seems that the most natural way of choosing renormalization scale is to separate Lagrangian into physical Lagrangian and counterterms , like in Peskin & Schroeder's book, chapter 10.2, p.325, eq.(10.19), when discussing 4D $\phi^4$ theory, they define the the physical mass $m$ to be the position of pole of propagator, set field strength to $1$ and define the coupling constant $\lambda$ as the scattering amplitude at zero momentum at condition $s=4m^2,t=u=0$. The exact quote goes like:

My question is: after we have determine the renormalization scale using our observation data, how can we still move the renormalization scale, claiming that the physics does not change with renormalization scale and have renormalization group equation? if we define the renormalization scale using our observation, it seems to me that changing the scale will be equivalent to changing the condition we observe in the experiment, and the underlying physics might not necessarily be the same.

this answer and this answer mention that the renormalization scale have something to do with the energy scale of the system, yet if we change the energy scale of the system, it feels like we are also changing the underlying physics.

Answer 1

Generally speaking you can set whatever renormalization conditions you wish as long as your theory remains unitary and all that. For example with $\phi^4$ you can fix your renormalized $\lambda$ with

$$\Gamma^{(4)}(p_1,p_2,p_3,p_4)=-i\lambda$$ for any set of external momenta $p_i$. What this means is that your renormalized coupling constant $\lambda$ is a function of the renormalization scale momenta $p_i$, $$\lambda=\lambda(p_i).$$ For any set of momenta $p_i$ you can (at least in principle) measure $\lambda(p_i)$ from some experiment and from there you can predict $\lambda$ at any other set of momenta by calculating $\Gamma^{(4)}$. Changing the renormalizaiton scale simply amounts to using some other set of renormalization momenta.

The reason you might want to do this (and I think this is poorly explained in most QFT textbooks) is that choosing a renormalization scale close to the physical momenta of your scattering problem renders the loop corrections to $\Gamma^{4}$ small. So when operating close to the renormalization momenta, the tree-level diagram is a good approximation to the complete quantity (if such a thing actually exists, heh). If you're working with particles at 100 GeV, you might not want to use $\lambda$ defined at 0.23 eV because then the loop corrections will be quite big and you have to do more work.

What this also means is that $\lambda$ also gives you the general interaction strength at the renormalized momenta that it's defined at. If you can figure out how $\lambda$ changes with the renormalization scale, you can get a rough idea of how strong the interaction is at different energies.