Why do I get a different result if I flip a loop and then apply Kirchhoff's loop rule?

Question

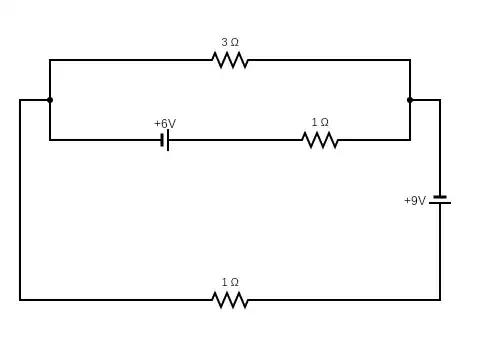
I've been practising to solve some exercises on electric circuits, especially using Kirchhoff's loop rule. Here I am asked to determine the intensity of the currents passing through each of the resistors.

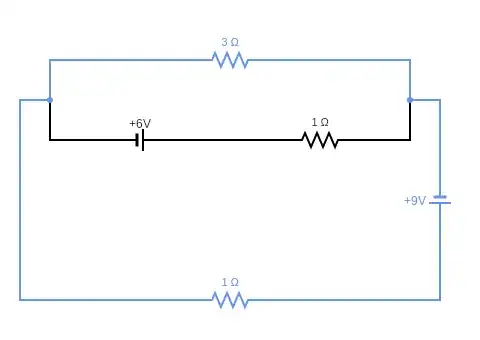
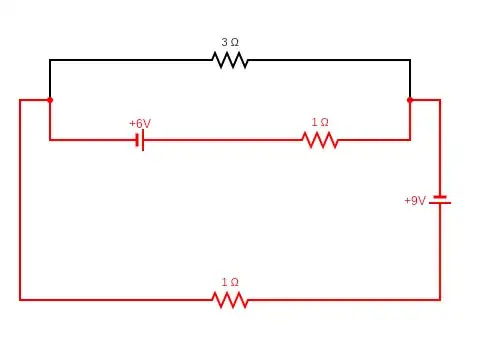
To solve the exercise, I have to focus on two independent closed loops. The rectangle on the top, containing two resistors and a cell, is clearly one of them. As for the second one, no matter which of the following two I consider, I get the same result (as I expected):

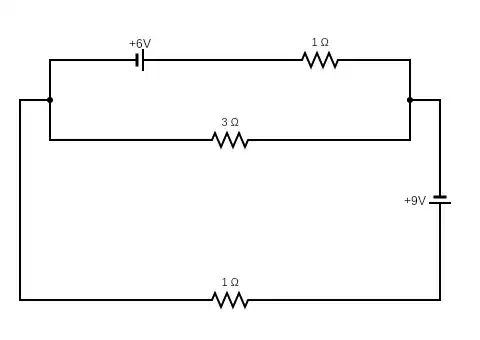
However, the circuit I was given made me think that the result should be the same if I physically flipped the loop on the top, with a $3D$ rotation:

Unfortunately, it looks like this is not the case, but I can't see how this simple geometric transformation could affect the current flowing in the small loop. In fact, after a bit of simplification, from the given picture (and the blue loop) one gets $$\begin{cases} 9-i_1+3i_2=0 \\ 6-i_1-4i_2=0 \end{cases} \\ \implies (i_1,i_2)=\left(\frac{54}7,-\frac37\right)$$ while for the flipped one $$\begin{cases} 15-i_1-i_2=0 \\ 6+3i_1-4i_2=0 \end{cases} \\ \implies (i_1,i_2)=\left(\frac{54}7,\frac{51}7\right)$$ (here $i_1$ is the current flowing through the red loop and $i_2$ the one flowing through the small circuit on the top).

I guess the shortcoming here lies in what I called $i_1$ and $i_2$. Precisely, I guess that they do not play the same role in the two situations. If this is the real problem, how to fix it? Can the flip be applied properly to get the same result?

Answer 1

Your mistake is a matter of relabelling.

Because there are two $1\Omega$ resistors, it is actually much more convenient to label the currents according to which battery they passed through. Since the two batteries are connected so that their voltages add up, it is clear that the currents are going to add up for them and traverse the loop in the direction that the batteries supply. Namely, the current $I_9$ goes down the $9\text V$ battery, left through the $1\Omega$ resistor, split up, $I_6$ of which goes rightwards through the $6\text V$ battery, right through the $1\Omega$ resistor, and that is one loop. Let the left-to-right current through the $3\Omega$ resistor be $I_3$

Then the loop I had just described goes as $$\tag1+9-I_9+6-I_6=0$$ There are two other loops, either $$\tag2+9-I_9-3I_3=0$$ or $$\tag3+6-I_6+3I_3=0$$ If you subtract Equation (2) from Equation (1), you will get Equation (3), so pick any two of the three of them will do.

You also need to conserve charge, i.e. conserve current, and that goes as $$\tag4I_9=I_6+I_3$$ If you now solve these set of equations, you will obtain $$\tag5(I_9,I_6,I_3)=\left(\frac{54}7,\frac{51}7,\frac37\right)\text A$$ which are all three numbers that you obtained. This means that your $i_1$ is my $I_9$ and you have two conflicting definitions of $i_2$; you could have fixed the issue yourself by invoking my Equation (4).

Or maybe your mistake is in assuming that there is only one single current flowing around the small loop. Either way, my answer should settle your problem.