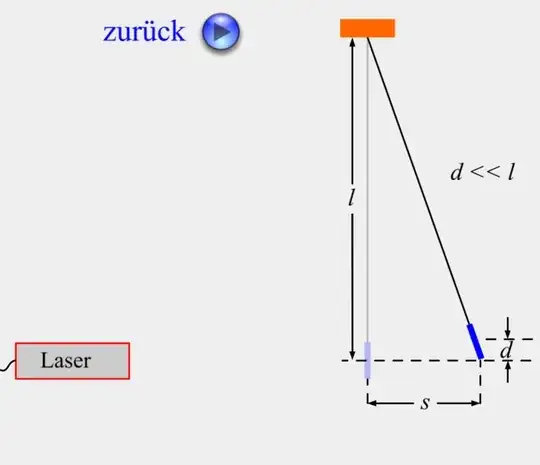
To experimentally verify the momentum of a photon, consider the illustration below. A photon pendulum.
Now, once the light hits the mirror, the momentum of the light is being transferred to the mirror. Depending on the momentum, the mirror will move with some velocity $v$ one can work out using conservation of energy.
Now my textbook claims using $$mgd=\frac{1}{2}mv^2$$ I may find the height $d$ the pendulum will swing. But the mirror on the pendulum with length l is constrained to stay inside a circle (approximately). Why is this approach valid, as a sufficiently large $v$ would let $h$ exceed the circle constraints?