Doubt About Euler Angles and Matrix Order Multiplication

Question

I'm asking this question here because the doubt comes from trying to understand a physical problem (kinematics of rotations), but this question would easily fit the MathExchange site also.

I was reading Chapter 4 - The Kinematics of Rigid Body Motion from the book Mechanics (3rd Edition) by Goldestein; more specifically pg. 152. I was trying to understand the notation of rotations and different representation in various frame of reference, whose notation I find very confusing.

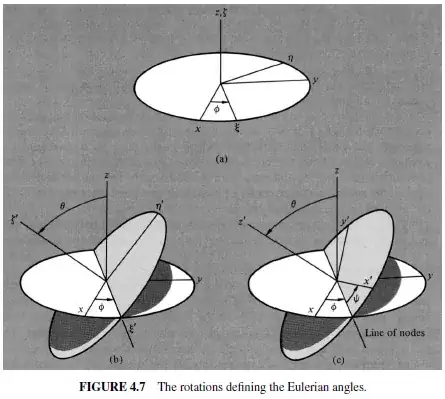
Goldestein starts explaining that we need three independent rotations to completly rotate an object.

First we rotate the $xyz$ axis to $\xi \eta\zeta$. Then from $\xi \eta\zeta$ to $\xi '\eta'\zeta '$ and finally from $\xi \eta\zeta$ to $x'y'z'$.

The first rotation about $z$ can be expressed as: $$ \boldsymbol \xi = D \mathbf x $$

The second rotation: $$ \boldsymbol \xi ' = C \boldsymbol \xi $$

And the last rotation: $$ \mathbf x ' = B \boldsymbol \xi ' $$ Hence, the matrix of the complete transformation is: $$ \mathbf x' = A \mathbf x $$ where $$ A = B C D $$ Until now everything make sense.

Then, the inverse transformation from body coordinates to space axes follows as: $$ \mathbf x = A^{-1} \mathbf x' $$

This stops to make sense to me. As from what I understand, I interpret a rotation as a set of displacements of points by an angle that conserve lengths. This points were initially on world space and after the rotation they are still on world space. Why would a change of basis would be needed?

I would interpret the equation $\mathbf x' = A \mathbf x$ as: "I know where the point $\mathbf x$ was before the rotation. Then I apply rotation $A$, to get where $\mathbf x$ is now after the rotation (given by $\mathbf x'$)". Why after applying a rotation now we are "seeing" things from the body point of view?

The matrix $A$ is completely expressed in body coodinates as this answer suggests. But why?

And also, Goldestein states that, for example, the matrix $D$, which he writes as: $$ D = \begin{pmatrix} \cos \phi & \sin \phi & 0 \\ -\sin \phi & \cos \phi & 0 \\ 0 & 0 & 1 \end{pmatrix} $$ is a counter clockwise rotation, but clearly: $$ \begin{pmatrix} \cos \phi & \sin \phi & 0 \\ -\sin \phi & \cos \phi & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} \cos \phi \\ -\sin \phi \\ 0 \end{pmatrix} $$ the cartesian basis is being rotated clockwise. As this post and this post might hint, this must be a problem of basis representation of the linear maps but the notation is confusing me.

I would be pleased if someone could reconcile both points of view, clarify how to know when we are expressing things from the body axis or from the global axis, and when the changes of basis is needed.

EDIT: I also found this answer, which also adds another interpretation to rotations. This question explanation agrees with what I said about how I interpret rotations. So now there is one more interpretation... Which one is correct, or how could we reconcile both views?

Answer 1

There are two ways to view a coordinate transformation as it applies to vectors: an "active" and a "passive" one.

In the "active" one, we think of the vector as going through some transformation while staying "within" the same coordinate system (or reference frame if you'd like). So only its components change, and that can reflect a rotation around an axis, among other things.

However, when we want to keep track of the relation between two distinct coordinate systems, we must take the "passive" view for the operation to make sense. In that case, we treat the vector more geometrically in the sense that it is always the same object, only expressed in terms of different components and basis vectors in the two coordinate systems. The transformation is then seen to be acting on the coordinate system, not on the vector, so that indeed as a geometric entity it must remain unchanged/passive under such a transformation.

For example, let $\mathbf{R}$ be a rotation operator, and $\boldsymbol{\vec{v}}$ an Euclidean vector in $\mathbb{R}^3$. Let $\{\vec{e}_i\}$ and $\{\vec{E}_i\}$ be two distinct basis sets for $\mathbb{R}^3$. Obviously, $\mathbf{R}$ then acts on the basis when considering a passive transformation. We will show that it follows that the inverse transformation must act on the vector components (which is also the origin of the terms co- and contra- variance). So if we act passively with the rotation matrix on the basis vectors we get:

\begin{align*} \boldsymbol{\vec{v}} &= v_1\vec e_1 + v_2\vec e_2 + v_3 \vec e_3 \\&= V_1\vec E_1 + V_2\vec E_2 + V_3\vec E_3 \tag{1} \\&= V_1R \vec e_1+V_2 R\vec e_2 + V_3 R\vec e_3 \\&= \boldsymbol{\vec{v}} \end{align*}

Now many authors will write $\boldsymbol{\vec{v}\ '}$ when referring to $(1)$ to mean "$\boldsymbol{\vec{v}}$ written relative to $\{\vec{E}_i\}$", but this is a slight notational abuse because as mentioned $\boldsymbol{\vec{v}}$ is a geometric object; it has no inherent dependence on the chosen basis, but our transformation acts exclusively on the basis. So while one may write that one should also remember that in fact $\boldsymbol{\vec{v}\ '} = \boldsymbol{\vec{v}}$.

Now the reason why one may feel more comfortable with this slight notational abuse is that one can always pretend that actually, we are acting with an active transformation, and that we are interested to change the vector within the same coordinate system. Because often we really do want to focus only on how the components change, we may for a moment treat the transformation as active. However, we can never really completely abandon the notion of the passive transformation because without it, we have no way to discuss relations between frames, i.e. "body frame" vs. "world frame".

To see that, act with $\mathbf{R}^{-1}$ on both sides of $(1)$, and recall that the $V_i$ here are just numbers so:

\begin{align*} \mathbf{R}^{-1}\boldsymbol{\vec{v}} &= \mathbf{R}^{-1}\left(V_1\mathbf{R} \vec e_1+V_2 \mathbf{R}\vec e_2 + V_3 \mathbf{R}\vec e_3 \right) \\&= V_1 \mathbf{R}^{-1}\mathbf{R} \vec e_1+V_2 \mathbf{R}^{-1}\mathbf{R}\vec e_2 + V_3 \mathbf{R}^{-1}\mathbf{R}\vec e_3 \\&= V_1\vec e_1+V_2\vec e_2+V_3\vec e_3, \tag{2}\end{align*}

we see that indeed an explicit active transformation on $\boldsymbol{\vec{v}}$ with $\mathbf{R}^{-1}$ is what recovers the components of the vector in the transformed basis $\{\vec{E}_i\}$. But this is only a kind of a mathematical trick, because the object we end up with, which mixes transformed components $V_i$ with untransformed basis vectors $\vec{e}_i$ is really of no geometric meaning if we want to relate two distinct coordinate systems. So geometrically the actual transformation under consideration is passive, as given by $(1)$, while $(2)$ is just a handy way to recover transformed vector components.

Note that Goldstein explains what I wrote in the last couple of paragraphs in some more detail in Pages 142-143, I recommend rereading it after this.

Finally, I believe all this will allow you to also solve the mystery of why the rotation applied to the components is clockwise relative the $z$ axis. If $\mathbf{R}$ is counterclockwise and it is the operator applied to the basis, then $\mathbf{R}^{-1}$ must be clockwise, so the latter is what acts on the components. What we're essentially doing often (and Goldstein does in that part of the book) is to take $\mathbf{R}^{-1}$ as an active transformation, only insofar as to be able to discuss how the components are related between the world frame and the body frame. But really to make sense of the connection between the frames we must always remember that it is $\mathbf{R}$ that acts on the basis vectors.

Answer 2

This a common confusion that arises in rotational dynamics. Rotations can be represented as tensors, by definition and construction invariant objects under change of coordinates. Tensors can be written as linear combination of a basis, and the coefficients of the linear combination are defined as the components of the tensor in the basis used.

Invariant nature is attained with components of the tensors transforming with the inverse transformation w.r.t. the basis.

Rotation tensor

Now, let's do a simple example: diven 2 Cartesian bases $\{ \hat{e}^0_i \}_{i=1:3}$, $\{ \hat{e}^1_j \}_{j=1:3}$, its possible to write the vectors of basis $1$ w.r.t. the vectors of basis $0$,

$$\hat{e}^1_i = \hat{e}^1_i \cdot \hat{e}^0_k \, \hat{e}^0_k = R_{ki} \, \hat{e}^0_k \ ,$$

and recast this expression using rotation tensor, whose components are defined as $R^{0 \rightarrow 1}_{ij} = \hat{e}^0_i \cdot \hat{e}^1_j$,

$$\mathbb{R}^{0 \rightarrow 1} = R_{ij}^{0 \rightarrow 1} \hat{e}^0_i \otimes \hat{e}^0_j = R_{ij}^{0 \rightarrow 1} \hat{e}^1_i \otimes \hat{e}^1_j $$

as

$$\hat{e}^1_i = \mathbb{R}^{0 \rightarrow 1} \cdot \hat{e}^0_i \ ,$$

as it can be easily proved by direct computation

$$\hat{e}^1_i = \mathbb{R}^{0 \rightarrow 1} \cdot \hat{e}^0_i = R_{kj}^{0 \rightarrow 1} \hat{e}^0_k \otimes \underbrace{\hat{e}^0_j \cdot \hat{e}^0_i}_{\delta_{ij}} = R_{ki}^{0 \rightarrow 1} \hat{e}^0_k = \hat{e}^0_k \cdot \hat{e}^1_i \, \hat{e}^0_k = R_{ki} \hat{e}^0_k \ . $$

Inverse rotation

Relation between a rotation and its inverse is represented by its transpose,

$$\begin{aligned} \hat{e}^1_i & = \mathbb{R} \cdot \hat{e}^0_i = R_{ki} \hat{e}^0_k \\ \hat{e}^0_i & = \mathbb{R}^T \cdot \hat{e}^1_i = R_{ik} \hat{e}^1_k \end{aligned}$$

Same vector, rotated basis

Vector $\vec{v} = v_0^i \hat{e}^0_i$, w.r.t. the rotated basis

$$\begin{aligned} \vec{v} = \underbrace{v_0^i \, R_{ik}}_{ = v_1^k} \hat{e}^1_k \qquad \rightarrow \qquad v_{1}^k = R_{ik} v_0^i && (1) \end{aligned}$$

Rotated vector, same basis

Rotating vector $\vec{v}$ with rotation tensor $\mathbb{R}$ gives the vector

$$\begin{aligned} \vec{v}^{Rot} = \mathbb{R} \cdot \vec{v} = R_{ij} \hat{e}_i^0 \otimes \hat{e}_j^0 \cdot (v_0^k \hat{e}^0_k) = R_{ik} v_0^k \hat{e}_i^0 \qquad \rightarrow \qquad v^{Rot, i}_0 = R_{ik} v_0^k && (2) \end{aligned}$$

As it can be easily realized, transformations (1) and (2) involves the rotation tensors and its transpose.