How can heat pumps be more efficient than electric/resistive heating?

Question

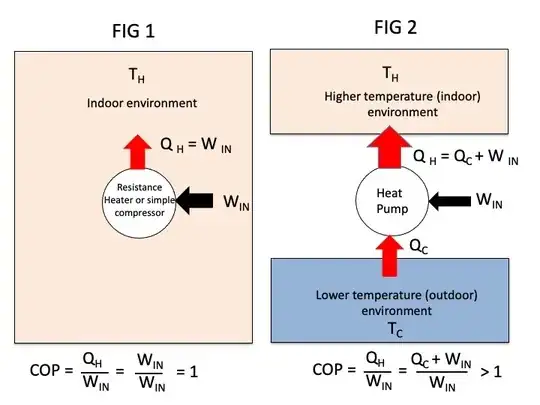
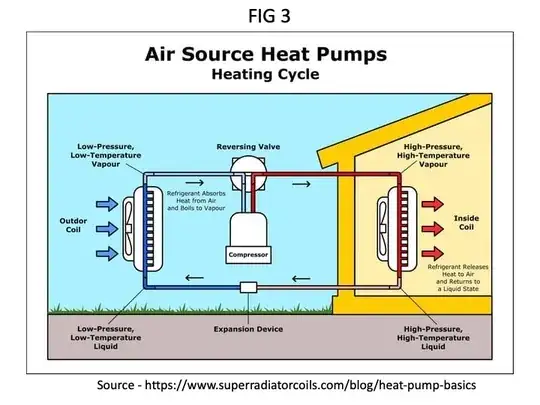
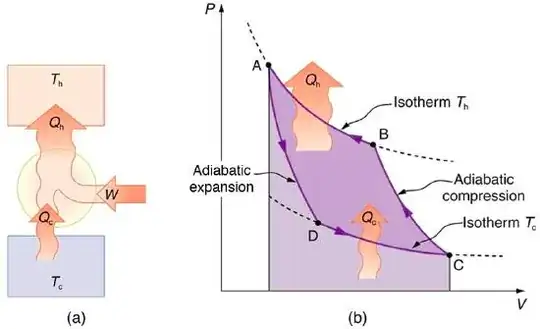
I cannot understand how a $COP > 1$ does not contradict the laws of thermodynamics (the first one, in particular).

Whatever searches I do, return things like "a heat pump is moving heat, not creating it" .... The answer in my mind is: "Yea, cute phrasing, I don't care: as far as I can see, the mechanism violates the first law of thermodynamics".

My understanding is that a heat pump is essentially (conceptually) like a fridge, or like an air conditioner, only that it is "cooling down the outside" (which is colder).

Using a simplified mode of operation where the operations are "lumped" or "discrete". Also to simplify, let's assume that the outside and inside temperatures are the same, $T$; the outside is considered to have an infinite amount of air, so its temperature will not change by the operation of our pump.

So, in my mind, the thing would go like: take a container with some gas; we mechanically compress it by spending an amount of work $W$. Then:

$(1)$ By the first law of thermodynamics, the amount of heat $Q$ that the gas got is exactly the amount of mechanical work that we applied to compress it; $Q = W$.

So, we now wait until it complete cools down. It cools down to approximately $T$ (the amount of air inside and its heat capacity far exceeds the amount of gas that we compressed).

Now we take it outside and let it expand, which does by doing a mechanical work of exactly $W$, and by the first law of thermodynamics, it will cool down by releasing an amount of heat of exactly $Q$.

We let it warm up and reach temperature $T$.

The cycle now repeats.

We spent exactly $W$ energy, and injected an amount of heat $Q_{IN} = Q = W$. As far as my understanding goes, $Q_{IN}$ cannot be greater than $Q$ and thus greater than $W$.

The simplifications actually work in the pump's favor. If the temperature outside was colder, the efficiency would actually be lower.

So, what am I missing? (I know that the actual operation is based on a continuous compressor and a valve, with heat exchangers in the path — but my understanding is that this is representative of how that setup works, just easier to visualize — is this assumption mistaken?)

Answer 1

The COP is simply "how much heat can I move for a given input of work." It is somewhat like saying "how many tons of coal can I move with a locomotive engine of X horsepower." The answer depends on the design of the engine and the tracks, etc. But the weight of the load and the power of the engine are not directly commensurate or comparable. You could say "I moved 100 tons of coal, which if burned has an energy content many times greater that the diesel fuel used to move it." That may be true, but it is not saying anything profound about conservation of energy.

If I were trying to heat a home by installing a duct connected to the inside of a volcano, I could transfer heat with an enormous COP simply by turning on a fan within the duct.

The answer you mentioned, "a heat pump is moving heat, not creating it" (or I should say, not only creating it) is simple and correct, and can be taken at face value.

Answer 2

None of the existing answers mentions entropy, but entropy generation vs. entropy transfer is arguably the key to understanding the distinction between resistive heating and a heat pump, and to understanding how the latter provides a coefficient of performance greater than 1.

This answer does not use "heat" as a noun anywhere. The reason is that the term is oversubscribed, as it were, and used colloquially and even in technical discussions to refer variously to energy, energy transfer, thermal energy, temperature, enthalpy, and entropy. This causes endless confusion. The working fluid of a heat pump does not need to transfer net energy to the region to be heated. What it must do is transfer net entropy.

The key points are as follows:

• Entropy is generated during any irreversible process, such as resistive heating.

• Entropy is also the “stuff” that shifts during heat transfer, analogous to matter shifting during mass transfer, volume shifting during pressure–volume work, and charge shifting during electrical work, for example.

• Matter also carries its own (state-dependent) entropy.

• If we wish to raise a region's temperature sustainably—meaning without compressing it indefinitely or packing more matter into it indefinitely—we must provide entropy. This can be done by generating entropy (through resistive heating, say) or by importing it (through a heat pump that brings in matter in a high-entropy state and moves out the same amount in a low-entropy state, say).

Intuitively, it takes nearly zero energy to roll a high-entropy material next to you, correct? The heating provided per required energy input would be very high, correct? This is essentially what a heat pump does, in a somewhat more sophisticated manner (e.g., by condensing high-entropy gas near you, which dumps entropy, and then pumping the resulting low-entropy liquid elsewhere and allowing it to vaporize again, which draws entropy from the surroundings).

Whereas a resistive heater requires temperature-increasing entropy to be produced entirely at the target, a heat pump uses clever engineering (and less work) to shift it from somewhere else. This translates into a relatively high efficiency. Energy is still conserved, and total entropy never decreases, so the laws of thermodynamics remain satisfied.

Thank you to @hyportnex for suggesting a summary of the math. When we seek to heat a target—hotter than the surroundings—by a small amount $\delta Q = T_\text{hotter}\,dS$, we could do completely dissipative electrical work $\delta W$ on an idealized resistor ($\delta W=\delta Q$). Or, we could (1) drive heat transfer to a working fluid from the surroundings to shift the same amount of entropy $dS$, with corresponding energy transfer $T_\text{colder}\,dS$, and (2) drive heat transfer from the working fluid to the target, with corresponding energy transfer $T_\text{hotter}\,dS$. (The specific driving mechanism can be any that tends to reversibly change the working fluid's temperature: compression, a chemical reaction, a phase change, polarization, magnetization, etc.) Since $T_\text{hotter}>T_\text{colder}$, conservation of energy requires us to provide at minimum an additional $(T_\text{hotter}-T_\text{colder})\,dS$ in the form of work for this cycle to be thermodynamically feasible. This is smaller than the work $T_\text{hotter}\,dS$ required by the resistive heater, yielding a relative advantage or coefficient of performance of at most $\frac{T_\text{hotter}}{T_\text{hotter}-T_\text{colder}}$.

So what's wrong with your calculation that the heat pump did work $W$ and provided heating $Q=W$, apparently no different from a resistive heater? The difference is that you could have collected the work $W$ that the gas did while expanding outside. The coefficient of performance in practice would then be limited only by friction and other dissipative mechanisms and by the tendency of the room to heat up.

Answer 3

I think all the current answers are missing that your problem is a terminology/definition issue.

The crux of your confusion should be at

Yea, cute phrasing, I don't care: as far as I can see, the mechanism violates the first law of thermodynamics

For all definitions of CoP, efficiencies, and so forth, the relevant and always-correct definition is $$\tag1\text{CoP, efficiencies }\eta,\text{ etc.}\quad:=\frac{\text{wanted output}}{\text{supplied input}}$$

Let us specialise to the Carnot cycle for convenience of exposition. As you are definitely familiar with, the efficiency of a heat engine is then $$ \begin{align}\eta \tag2&=\frac W{Q_H}\\ \tag3&=\frac{Q_H-Q_C}{Q_H}\qquad\text{by Conservation of Energy}\\ \tag4&=1-\frac{Q_C}{Q_H}\\ \tag5&=1-\frac{T_C}{T_H}\qquad\text{Carnot cycle}\\ \tag6&<1 \end {align} $$ as expected.

But when running the exact same Carnot cycle device as a heat pump, you want $$ \begin{align}\text{CoP} \tag7 &=\frac{Q_H}W\\ \tag8 &=\frac{Q_H}{Q_H-Q_C}\qquad\text{by Conservation of Energy}\\ \tag9 &=1+\frac{Q_C}{Q_H-Q_C}\\ \tag{10}&=1+\frac{T_C}{T_H-T_C}\qquad\text{Carnot cycle}\\ \tag{11}&>1 \end {align} $$ Because the $1^\text{st}$ law of thermodynamics is exactly equivalent to the conservation of energy, what I have written down is thus a direct refutation of your assertion that there is any violation at all. You are simply being too cavalier about the definitions and worked yourself into a corner.

Answer 4

Now we take it outside and let it expand, which does by doing a mechanical work of exactly $W$, and by the first law of thermodynamics, it will cool down by releasing an amount of hear of exactly $Q$.

OK. First we did mechanical work $W$ on gas, and the we got mechanical work $W$ out of the gas. So the net energy we used was zero. So COP was infinite. Outside thermal energy was moved inside, using zero energy.

I do not see energy created or destroyed here. What is the problem?

Answer 5

Yea, cute phrasing, I don't care: as far as I can see, the mechanism violates the first law of thermodynamics

It's healthy to be skeptical but assuming you've experienced air conditioning, you must have observed that it works. If your description of the cycle were correct, it wouldn't work. A heat pump is essentially an air conditioner in reverse (which can also work as an air conditioner.)

Now we take it outside and let it expand, which does by doing a mechanical work of exactly W, and by the first law of thermodynamics, it will cool down by releasing an amount of hea[t] of exactly Q

I think this is where your understanding goes sideways. Heat is not released to the larger environment in this phase. Heat is absorbed from the outdoors.

Let's step back a minute. You are in an enclosed space and have a container which you mechanically compress gas into. As you correctly explain, the container heats up and that heat is a result of the work W you put into compressing the gas. You wait as it cools. It cools because it is hotter than the room you are in, so the heat that was produced flows into the room, warming the room. This heat Q is greater than zero but less than W because once the room and the container reach the same temperature, the flow stops.

Now consider what happens if you release the pressure on the container. It will become cooler than the room. The heat from the room will flow back into the container. If you repeat this process, you will warm the room over time due to the work being put into compressing. This method of heating will have an efficiency limit of 1 just like a resistance heater.

Now go back to the quoted claim above. According to your claim 'it will cool down by releasing an amount of hea[t] of exactly Q'. That can't be correct. We already released some amount of energy Q1 where 0 < Q1 < W. We can't release an addition al Q2 = W worth of energy. That would mean the total Q (Q1 + Q2) is greater than W. That's what we call a perpetual motion machine. In other words, it can't work the way you describe because that would be a violation of the laws of thermodynamics.

So now consider if we release the pressure outside. The container cools to some temperature below that of the outdoor temperature. This causes heat to flow from the outdoors into the container. The container absorbs heat from outside. You then take that container inside and bring that absorbed heat with it. You now compress that container, it becomes hotter than indoors and heat flows to the room from the container. On each repetition, you are absorbing heat from outdoors and releasing it to the room. That is the heat you are 'moving'.

Answer 6

I'm not sure I follow the reasoning on your cycle, but I think I understood some of the confusion in your comments.

Look at net energy of the system. We have heat in $(Q_{\text{in}})$, heat out $(Q_{\text{out}})$, and work in $(W_{\text{in}})$. We know $Q_{\text{out}}$ is opposite sign to the others. We get:

$$Q_{\text{out}} = Q_{\text{in}} + W_{\text{in}}.$$

And if we're heating, we only care about $Q_{\text{out}}$ and $W_{\text{in}}$ for COP. If $Q_{\text{out}}$ and $Q_{\text{in}}$ are close to each other, $W_{\text{in}}$ can be much lower than $Q_{\text{out}}$, giving a COP above $1$.

$W_{\text{in}}$ is not directly equal to $Q_{\text{out}}$ or $Q_{\text{in}}$ either. The heat gained and lost have to do with the temperature on both sides of the coils, compared to the temperature of the refrigerant in the cycle at the coils. By using phase changes and pressure differences, the refrigerant can have quite a difference between hot and cold sides, so both can transfer a lot of heat to their respective surroundings.

Answer 7

The key point with the reversed Carnot cycle, working as a heat pump (which is not how real heat pumps usually work) is that when the working medium is expanding, we can recover some of the work we put in during the compression. This is because the expanding medium, during isothermal expansion, converts internal energy of the outside immediately to work. This decreases our work cost per cycle $W_{cycle}$ so it is actually smaller than the work $W$ we spend during the compression phases.

Details: if we idealize the heat pump heating up hotter room using a colder atmosphere outside via a reversed Carnot cycle, we have four stages for the working medium:

I. (inside) adiabatic compression, work done on the medium is $W_{ad}$;

II. (inside) isothermal compression at higher $T_2$, work done on the medium is $W_2$;

III. (outside) adiabatic expansion, work done on the medium is $W_{ad}'$ (negative);

IV. (outside) isothermal expansion at lower $T_1$, work done on the medium is $W_1'$ (negative).

The only stage where heat can flow into the room is II. ( isothermal compression). In case the working medium is ideal gas, the heat released is $Q_H = W_2$, and it diffuses to the whole room and heats it up.

But the work spent per cycle

$$ W_{cycle} = W_{ad} + W_2 + W_{ad}' + W_1' $$ is smaller, because $W_{ad}' + W_1'$ is negative (we recover some of the work spent during compression).

Thus $W_{cycle} < W$, because we extract some work from the outside in each cycle.

Heat released $Q_H=W_2$ is smaller than $W$ too, but it is still greater than $W_{cycle}$:

$$ W_{cycle} < Q_H < W. $$

So contrary to the intuitive idea of a heat pump, it is not necessarily true that the heat pump medium absorbs heat from outside and then dumps it inside. It may very well be (it is in the idealized case where the medium is ideal gas and the cycle is the reversed Carnot cycle) that the cooled medium from outside is actually not bringing any energy inside, but instead, its expansion outside is allowing the pump to turn some energy of the outside into useful work and thus decrease the work cost.

Answer 8

You're missing that heat pumps don’t turn electricity into heat — they move heat from one place to another, using that electricity to run a cycle that pulls in more heat than the energy it consumes. So if you spend 1 unit of energy to move 3 units of heat from outside to inside, your Coefficient of Performance (COP) is 3 — and no laws are broken because you're not creating energy, just relocating it. It's like paying \$1 to carry \$3 worth of groceries into the house — you didn’t make more groceries, you just used smart effort to move them.

Answer 9

The short answer to the title of your post is the following:

Resistance heating converts electrical work into heat into the environment intended to be heated. The electrical work of the heat pump is also converted to heat but it is in addition to the heat it moves from the cold environment to the environment intended to be heated due to the heat pump cycle.

Bottom line: For the same electrical energy input, the heat pump delivers more heat to the environment intended to be heated than a resistance heater. That means a resistance heater has a COP of 1, while a heat pump has a COP greater than 1

Hope this helps.

Answer 10

So, in my mind, the thing would go like: take a container with some gas; we mechanically compress it by spending an amount of work $W$. Then:

(1) By the first law of thermodynamics, the amount of heat $Q$ that the gas got is exactly the amount of mechanical work that we applied to compress it; $Q = W$.

First of all, the gas didn't "get" heat $Q$ due to the compressor work. The compressor increases the internal energy $U$ (and thus temperature $T$) of the gas due to the mechanical compression work. As a result of the temperature increase of the gas relative to the environment (and assuming it is allowed to transfer heat to the environment), heat then flows from the gas to the constant temperature environment until the gas temperature is lowered to that of the environment.

From the first law for a closed system.

$$\Delta U=Q-W$$

If the system is insulated, or the compression happens very fast before heat transfers out, the first step is then, for an ideal gas

$$\Delta U_{1}=W=C_{v}\Delta T=C_{v}(T_{gas}-T_{env})$$

Work ceases and now heat is allowed to transfer to the environment (step 2), or as you say, we allow it to cool down to the temperature of its environment. From the first law

$$\Delta U_{2}=Q=C_{v}(T_{env}-T_{g})$$

Cooling down causes the internal energy to decrease. This decrease equals the increase in internal energy during compression, such overall total change in internal energy is zero (energy is conserved) between the two steps since

$$\Delta U_{tot}=\Delta U_{1}+\Delta U_{2}=C_{v}(T_{gas}-T_{env})+C_{v}(T_{env}-T_{gas})=0$$

Thus the overall effect of the two steps is the work done on the gas equals the heat from the gas to the environment or

$$Q=W$$

The COP of a refrigerator or heat pump is defined as the ratio of the desired heat transfer, in this case the heat transferred to the indoor environment, to the work required to cause the transfer, which for a compressor is mechanical (though ultimately, as correctly pointed out by @Chet Miller in his answer, electrical for the utility service). Since the two are equal, the COP is 1.

The above is shown in FIG 1 below. Note that it applies to both the compressor and an electrical resistance heater. The only difference is the immediate "work" input is electrical work for the resistance heater and mechanical work for the compressor.

Now let's replace this simple compressor with a "system" which we call a "heat pump" consisting of a compressor, condenser coil (indoors) and evaporator coil (outdoors) and expansion device as shown in FIG 3 taken from this site: https://www.superradiatorcoils.com/blog/heat-pump-basics. The energy flows are shown in FIG 2.

Note that now, in addition to the compressor causing heat transfer to the warm environment directly due to its mechanical compression work, at its high pressure output side in the diagram, it now also facilitates the absorption and transfer of heat by the evaporator in the external environment at its low pressure input side. There is no overall violation of the first law since overall the energy input to the cycle ($Q_{C}+W_{IN}$) equals the energy output of the cycle ($Q_{H}$) with the change in internal energy of zero for a complete cycle.

If the temperature outside was colder, the efficiency would actually be lower.

That is in fact correct, when we equate the COP of the heat pump cycle to its efficiency. It accounts for the fact that heat pumps are less efficient in colder climates. This can be seen by taking the COP of an ideal Carnot heat pump which is described in terms of the indoor and outdoor temperatures as

$$COP=\frac {T_{H}}{T_{H}-T_{L}}$$

For a given $T_{H}$, the lower $T_{L}$ the lower the COP.

It makes sense if you think in terms of the greater amount of work needed to lift a given amount of weight the greater the height as being analogous to moving a given amount of heat over a greater temperature difference (height).

Hope this helps.

Answer 11

A heat pump works by taking advantage of the physical properties of a refrigerant. Those properties are:

a boiling point that is somewhat below the target temperature (although boiling point can be adjusted by adjusting the pressure appropriately), a high heat of vaporization, a moderate density in liquid form, a relatively high density in gaseous form (which can also be adjusted by setting pressure appropriately), and a high critical temperature.

— Refrigerant: Requirements and Desirable Properties, Wikipedia

In a heat pump system, the refrigerant is forced into a gaseous phase in the evaporator, and forced into a liquid phase in the condenser. This is done by controlling the pressure of the refrigerant at the two ends of the system using a compressor motor.

In order for a liquid to evaporate, it must absorb its latent heat of vaporization; and in order for a gas to condense, it must release that latent heat. The latent heat is essentially the energy required to “keep the gas gaseous.”

You've likely experienced this phenomenon when boiling water in a pot—you bring the water up to 100°C, and then it has to sit and absorb more heat as liquid water evaporates into water vapor. That extra heat energy is held in the water vapor, even though it didn't raise its temperature beyond 100°C.

The heat pump uses a compressor to run its refrigerant through a loop of pipe. The pipe has a restriction that causes the pressure to be higher at the condenser and lower at the evaporator. In the low-pressure evaporator, the liquid refrigerant evaporates because its temperature is above its boiling point for the given pressure. In order to evaporate, it absorbs its latent heat of vaporization from the environment. That heat energy is then stored in the now-gaseous refrigerant. And in the high-pressure condenser, the gaseous refrigerant condenses because its temperature is below the boiling point for the given pressure. In order to condense, it releases its latent heat of vaporization into the environment.

Importantly, the only work the heat pump does is to run a compressor to pump the refrigerant through the pipe loop, which also maintains the high and low pressures thanks to the restriction in the pipe. The refrigerant evaporates as a completely natural side-effect of its temperature and pressure, and the latent heat of vaporization that it absorbs comes from the surrounding environment as it flows through the evaporator—helped by increasing the surface area of the pipe with lots of metal fins.

So in that sense a heat pump really is “pumping heat energy,” using the refrigerant to store it. If you can move enough heat energy by cycling enough refrigerant quickly enough, you can move more heat energy per minute than it takes to run the compressor.

As a concrete example, consider a particular refrigerant: R-134a, a.k.a. Freon. According to these Thermodynamic Properties charts for Freon, 1kg of R-134a has latent heat of vaporization of 182.5kJ at 20°C. Say it takes 1kW, or 60kJ/min, to run the compressor. Then a perfectly efficient heat pump that cycled that 1kg of R-134a once per minute could move 182.5kJ of heat per minute if inside and outside were both at 20°C, and could have a COP of just over 3.0.

Answer 12

By the first law of thermodynamics, the amount of heat Q that the gas got is exactly the amount of mechanical work that we applied to compress it; Q=W

In British English, "got" can mean "has" or "received", so in the interest of reducing ambiguity, I think we should avoid that word.

(I know that the actual operation is based on a continuous compressor and a valve, with heat exchangers in the path — but my understanding is that this is representative of how that setup works, just easier to visualize — is this assumption mistaken?)

As stuffu said in their answer, if that were what it was based on, then it would, theoretically, be possible to recover the work when the gas expands; it would not violate thermodynamic laws to expend no energy. It would, however, not be possible practically to recover all (probably not even most) of the energy.

But a heat pump is not, in fact, based on compression and expansion cycles. If a heat pump were just compressing and expanding a gas, it wouldn't need a special chemical to use as refrigerant; it could use any gas. A heat pump is based on the following steps:

1. Find a chemical whose boiling point at standard pressure is slightly below room temperature.

2. Compress the chemical.

3. Allow the chemical to release its heat into the room.

4. The chemical is now at a higher pressure, so its boiling point is higher. With enough compression, the boiling temperature is higher than room temperature, so by the time the chemical reaches room temperature, it has condensed into a liquid, releasing heat into the room.

5. Take the chemical outside.

6. Release the pressure on the chemical. This lowers its boiling temperature back below room temperature, so it boils, drawing in heat from the outside.

7. Bring the chemical back inside.

8. Repeat steps 2-8

It is the phase transitions from gas to liquid and back again that transfer the heat. The heat exchanges of phase transitions are much, much larger than those of compression and expansion. For instance, water vapor condensing into liquid water will release around 2kJ/g, while water vapor cooling one degree Kelvin will release about one thousandth of that.

The compression and expansion are not directly transferring a significant amount of heat. The compression and expansion are just to put the chemical in a state where it will undergo those transitions. The less energy it spends on those steps, the higher the COP.

Answer 13

If we put all parts of the heatpump in a closed room the temperature rise will only be a function of how much energy we feed to the compressor. The ”total COP” when mixing the warm and cold air generated ought to be close to 1.

Answer 14

If you are trying to transfer heat from a heat source and to deliver work (mechanical energy), (as, for example, in the case of an engine) the parameter which really matters is the efficiency, defined as the work produced divided by the heat transferred from the heat source. High efficiency is desired.

If you are trying to do work in order to transfer heat to or from the surroundings, (as, for example your resistance heater or your heat pump), the parameter which really matters is the coefficient of performance, defined as the work done divided by the heat transferred to the portion of the surroundings receiving the heat (or, in the case of refrigeration, the heat removed from the portion of the surroundings being cooled). High coefficient of performance is desired.

In the case if your resistance heater, the coefficient of performance is $$\text{cop}=\frac{Q_h}{W}$$where $W$ is the electrical work expended by the resistance heater and $Q_h$ is the heat transferred to the room. But from the first law of thermodynamics, if the heater is operating at steady state and the room temperature is constant, $Q_h=W$ and the coefficient of performance is $$\text{cop}=1.$$

In the case or your heat pump, the coefficient is again defined as $$\text{cop}=\frac{Q_h}{W}.$$For an ideal heat pump operating reversibly and at steady state, the first- and second laws of thermodynamics tell us, respectively: $$W=Q_h-Q_c$$and$$\frac{Q_h}{T_h}=\frac{Q_c}{T_c}$$where $Q_c$ is the heat transferred from the cold heat source (the outside air) to the heat pump, $T_c$ is the temperature of the heat source, and $T_h$ is the temperature of the room air (into which the heat $Q_h$ is delivered). If we combine these equations, we obtain: $$\text{cop}=\frac{Q_h}{(Q_h-Q_c)}=\frac{1}{(1-T_c/T_h)}.$$This is clearly greater than one (the cop of the resistance heater). So its performance is superior.

We can also look at the rate of entropy generation with the resistance heater compared to the reversible heat pump. In the case of the ideal reversible heat pump, the rate of entropy generation is zero, while, in the case of the resistance heater, the rate of entropy generation is positive. This is another indication that, thermodynamically, the heat pump is superior.

Answer 15

Resistive heating
The first law of thermodynamics says that the energy transferred to the room is the Joule's heat. The second law of thermodynamics doesn't pose problem, but worth mentioning: the energy is transferred from a body with a very high effective temperature (power line/station) to a much colder room - no problem here, even if this looks very different from the traditional gas example given in textbooks.

Heat pump
The second law states that heat cannot be transferred from a colder body (here - outside) to a warmer body (here - inside of the room) without an extra work done. The work supplied by the power station permits transferring some heat from the environment to the room. In addition, the work itself originate from heat transfer from a hot body (power line/station) to a colder one (inside and outside of the room.) The sum of the heat transferred from the outside and that dumped in the room is the net heating effect - it is clearly limited by the efficiency of the heat transfer from the outside and the amount of heat dumped into the room... but it seems that there is no particular prohibition that it shouldn't greater than Joule's heat.

The following image seems like a good visualization of energy conservation in heat pump operation (image source):