I'm not versed at all in high energy physics, I come from a statistical mechanics background, hence, all of what follow is far from my comfort zone. I will also talk about what is, I believe, the lore of $\phi^4$ in statistical mechanics, perhaps things are different in high energy physics.
In the PSE post Is the 4D Ising model a second-order phase transition?, a comment says:
4$d$ $\phi^4$ [phase transition] is first order because of Coleman-Weinberg.
when arguing about the fact that while the lattice Ising model in $d=4$ has a continuous transition, the continuous (field theory) $\phi^4$ has a discontinuous transition. This clashes with a lot of things I took for granted, and I believe that a clear answer to the following questions would clarify the subject for me. I might have asked them in separated posts, but I think they do well together.
First, I always thought that continuous $\phi^4$ was the continuum version of lattice Ising, for example by mapping the discrete Ising model to continuous variable through a Hubbard-Stratonovich transformation, and expanding the obtained free energy. Moreover, we sometimes see the unstable critical line of $\phi^4$ named the QFT Ising one (see this book for example):
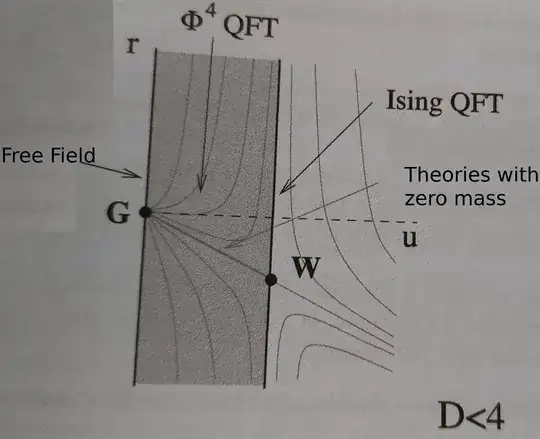Where the QFT is constructed by going against the flow of the Renormalization Group to send the cutoff to $\infty$ and obtain the continuous limit of the theory (in the sense that there is no cut-off). This is in $d<4$ but cannot the same be done for $d=4$ where now, the unstable line is at $u=0$ and where the WF and the Gaussian fixed point coincide?The RG group of a $\phi^4$ theory in $d=4$ predicts a critical point at ($r$ or $m^2$ or )$t=0$ and $u=0$ with the same exponents as the mean field theory but with logarithmic corrections to some observables due to the power law (instead of exponential) decay of the marginally irrelevant non-linearity. This seems to disagree with the fact that the transition should be discontinuous.
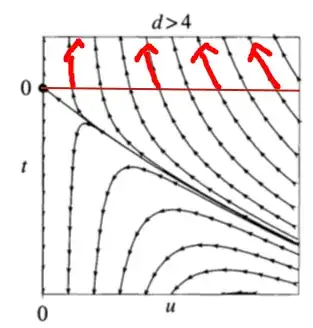
The way I naively understand the Coleman-Weinberg theorem, is that in some systems, a negative mass squared is generated along the RG flow when started from $m^2=0$. To me, this seems to be impossible with a $\phi^4$ theory as the common lore is that (thermal) fluctuations, decreases the critical temperature (restores the symmetry breaking for a small range of mass/temperature, instead of breaking it as required by the Coleman-Weinberg theorem). See for example this RG flow where $r\equiv t\equiv m^2=0$ points are mapped to large positive mass squared, except at the critical point:
This story seems to agree with the PSE post: How can quantum fluctuations lead to Spontaneous Symmetry Breaking?.
Maybe the problem resides in the fact that I'm not carefully treating $\Lambda\to \infty$ in all my points above?
