A brick sliding in an horizontal plane after an initial push (under Coulomb's dry friction and Stokes' drag) - part 3
Intro
This is a follow up of this question. After finding counter-intuitive the result given my little homemade experiment I tried to move forward and incorporated the air resistance.
Main section
$\DeclareMathOperator\sgn{sgn}$ Following this Wikipedia for friction under Coulomb damping | Illustration I should formulate Newton's 2nd law for a brick moving on an horizontal plane as (for positive constants $\{k,\ g,\ m,\ b\}$): $$my'' = -F-\sgn(y')kmg \label{Eq. 1}\tag{Eq. 1}$$ Considering $F=by'$ the air resistance as Stoke's drag and calling $\gamma = \frac{b}{m}$ by simplifying the mass I will get: $$y''=-kg\,\sgn(y')-\gamma y' \label{Eq. 2}\tag{Eq. 2}$$
Thanks to an amazing answer by @Nicolas and if a didn't messed up on this question, by considering the following finite extinction time $0<T<\infty$: $$T = \frac{1}{\gamma}\ln\left(1+\frac{\gamma |y'_0|}{kg}\right)\label{Eq. 3}\tag{Eq. 3}$$
and the distance traveled by the brick as: $$\Delta y = \frac{|y'_0|}{\gamma}-\frac{kg}{\gamma^2}\ln\left(1+\frac{\gamma |y'_0|}{kg}\right)\label{Eq. 4}\tag{Eq. 4}$$ the solution to \eqref{Eq. 2} should be described as: $$y(t) = y_0+\sgn(y'_0)\Delta y-\sgn(y'_0)\left[\frac{kg}{\gamma^2}e^{\gamma T}\left(e^{-\gamma t}-1\right)+\frac{kg}{\gamma}t+\Delta y\right] \cdot \theta\!\left(T-t\right)\label{Eq. 5}\tag{Eq. 5}$$
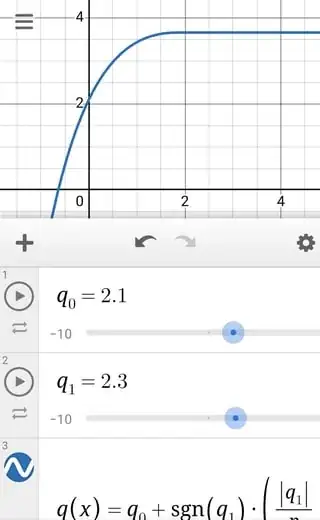
Here $y_0 := y(0)$, $y'_0:=y'(0)$, and $\theta(t)$ is the Heaviside step function. The solution of \eqref{Eq. 5} could be seen in this Desmos.
Question
I want to know how accurate is this model/solution for phenomena on daily life scales like the experiment I did: Could it be explaining the difference shown in the GIF compared with the results without Stoke's drag? (as @interstellar answer explains with only Coulombs' friction considered, both objects should have stopped at the same time and distances).
As example of what I mean with accuracy, if you do the experiment in a lab, with 95% significance level, making a confidence interval for the average of the difference between the forecast final position and the experimental results, Do zero get inside the interval? (So a Null hypothesis saying that there is no difference could not be rejected)... What is the standard deviation in centimeters? This for multiple attempts on the same object with same initial conditions... Do it holds for different initial speeds? Different objects?
Another idea would be do the experiment in the lab one time with good measures of the inital speed and then tune the constants such the model given by the solution of \eqref{Eq. 5} fits the real position vs time curve of expwriment: Will it forecast accuratelly the curve on another attempts? Will it fit also for different initial speeds?
Added later - not mandatory reading
discussion with @Eric in the comments
I tried what you mentioned. Unfortunately here I don't have any way to accurately measure the initial speed of the objects, but since they start with the same initial speed I tried to study the ratio between the ending positions.
A) scenario with model $y'' = -kg\sgn(y')$
In this case $\Delta y = \frac{|y'_0|^2}{2kg}$ (see $\text{Eq. 5}$ on the previous question), so if I want to compare the final distances for both objects I will have: $$\frac{\Delta y_1}{\Delta y_2} = \dfrac{\frac{|y'_0|^2}{2k_1g}}{\frac{|y'_0|^2}{2k_2g}} \overset{\text{both start with same initial speed }y'_0}{=}\frac{k_2}{k_1}\label{Eq. 6}\tag{Eq. 6}$$ the same proportion independently from the objects' masses and their identical initial speeds.
B) scenario with model $y'' = -kg\sgn(y')-\gamma y'$
Here the problem is harder since the final position is very nonlinear as could be seen from \eqref{Eq. 4}, so I will have in principle: $$\frac{\Delta y_1}{\Delta y_2} = \dfrac{\frac{|y'_0|}{\gamma_1}-\frac{k_1g}{\gamma_1^2}\ln\left(1+\frac{\gamma_1 |y'_0|}{k_1g}\right)}{\frac{|y'_0|}{\gamma_2}-\frac{k_2g}{\gamma^2}\ln\left(1+\frac{\gamma_2 |y'_0|}{k_2g}\right)}$$ here I had numerical problems with this formula when plotting the results, so I modified it a little be defining a parameter $\alpha = \frac{k_1}{k_2}\frac{\gamma_2}{\gamma_1}$, and variables $m=\frac{k_1g}{\gamma_1|y'_0|}$ and $n=\frac{k_2g}{\gamma_2|y'_0|}$, and noticing that $m = \alpha n$, I will have that: $$\frac{\Delta y_1}{\Delta y_2} = \underbrace{\frac{k_2}{k_1}}_{\text{Previous Eq. 6}}\cdot\underbrace{\alpha\cdot \dfrac{\left(1-\alpha n\ln\left(1+\frac{1}{\alpha n}\right)\right)}{\left(1- n\ln\left(1+\frac{1}{n}\right)\right)}}_{f(n,\alpha)}\label{Eq. 7}\tag{Eq. 7}$$
C) Homemade experiment parameters
From the Wikipedias Stokes' law I have that $\gamma = 6\pi\mu R$ with $R$ the radius of a spherical object, and $\mu$ the dynamic viscosity, which for air in Viscosity it is said at standard conditions it is equal to $\mu = 18.5\,[\mu Pa\cdot s]$.
The surface the stapler shown in the direction of movement was given by $s_1 = 30\text{ mm x }60\text{ mm} = 0.0018\text{ m}^2\equiv \pi R^2\Rightarrow R_1 = 0.024\text{ m}$ the equivalent radius. This leads to $\gamma_1 = 6\pi\mu R_1 = 8.37\cdot 10^{-6}\,[Pa\cdot s]$.
The surface the USB memory shown in the direction of movement was given by $s_2 = 40\text{ mm x }5\text{ mm} = 0.0002\text{ m}^2\equiv \pi R^2\Rightarrow R_2 = 0.008\text{ m}$ the equivalent radius. This leads to $\gamma_2 = 6\pi\mu R_2 = 2.79\cdot 10^{-6}\,[Pa\cdot s]$.
As you said, they are very tiny, but since their ratio is an important part of the formula for $f(n,\alpha)$ I don't see as obvious they are negligible $\gamma_1/\gamma_2 = 3$ (this because accidentally $R_1/R_2 = 3$ exactly).
From the wiki for Friction I found that the kinetic/sliding friction coefficient $k$ ($\mu_k$ in the website text) is shown in a table for some materials: $$\begin{array}{c | c}\hline \text{materials in contact} & k \\ \hline \text{Metal - Wood} & 0.49 \\ \text{Wood - Wood} & 0.32 - 0.48 \end{array}$$
Both the stapler and the USB memory have plastic bottoms, so the interaction is $\text{Plastic - Wood}$ but it was not listed, but just seen the table numbers, the range only for Wood is quite wide $0.48/0.32 = 1.5$ so following \eqref{Eq. 6} I could expect a $50\%$ of difference just with Wood (not too good from the accuracy point of view).
Unfortunately with this I got inconclusive results: I observed that for tiny pushes (slow initial speed), both objects move almost the same final distance, by I don't know if this is against the proportion law of \eqref{Eq. 6} or just because since the distances are too short I cannot distinguish visually if the proportion have worked but the difference it to small to notice it.
On the other hand, since both the stapler and the USB memory have plastic bottoms, I am thinking in something like $k_1 \approx k_2$ so under this assumption \eqref{Eq. 6} wouldn't be working here, but the problem is that when \eqref{Eq. 7} do could give the required difference between objects, $\gamma_2$ is so small that I believe the variable $n$ will be huge so $f(n,\alpha)\sim 1$ so it wouldn't be delivering neither the required difference.
With this analysis I think you are probably right and $k_1\neq k_2$ even when they are the same materiales involved, this would imply that the kinetic friction coefficient is somehow a constant which is characteristic for each object, not just dependent of which materials are interacting.
Since I just have to verify a proportionality relation, I will try again the same experiment with a measuring tape and two objects of different size and weight but made of the exactly same material: two pieces of wood from the same plank. I will share the results to comment what I found later.