Physical Description of a Coin. Equations and constraints

Question

I've been trying to describe the behaviour of a coin that can roll, spin and fall with Lagrangian Mechanics. The coin can roll without slipping with it's only "knowledge" of the floor being the contact point with it.

---

Description of the System:

The rotations and translations the system can have are the following:

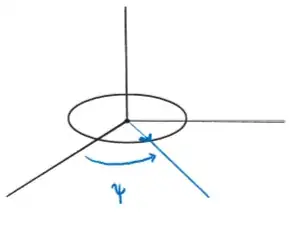
1. A rotation about the normal to the coin face $(\psi)$.
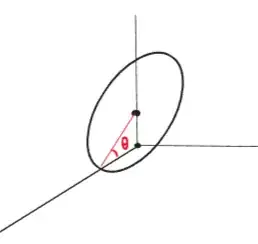
2. A rotation about a perpendicular axis to the coin face that transverses the edge of the coin $(\theta)$.
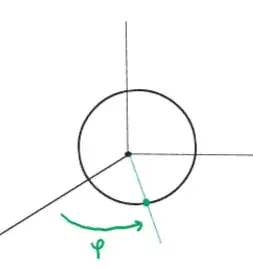
3. A rotation of the point of contact about the $z$ axis $(\varphi)$.
4. A translation of the center of mass of the coin.

Any point on the disk can be expressed in the lab frame of reference as: $$ \mathbf R = \mathbf R_0 + R_z(\varphi)R_y(\theta)R_z(\psi) \mathbf R' $$ where $\mathbf R'$ represent any point of the disk as seem form the disk itself and $\mathbf R_0$ represent the center of mass of the disk. $R_z(\varphi), R_y(\theta)$ and $R_z(\psi)$ represent the matrices of the rotations shown at the top.

The center of mass position is given by: $$ \mathbf R_0 = \begin{pmatrix} x \\ y \\ R \sin \theta \end{pmatrix} $$

where $x$ and $y$ are the projections of the position of the $CM$ to the $xy$ plane and $R$ represent the radius of the coin.

Now I can easily find the Lagrangian of the coin and get a description of the system:

$$ \boxed{ \\ \; \\ \mathcal L = \frac{1}{2} m \left ( \dot{x}^2 + \dot{y}^2 + R^2 \dot{\theta}^2 \cos^2 \theta \right ) + \frac{1}{2} I_{\psi} \dot{\psi}^2 + \frac{1}{2} I_{\theta} \dot{\theta}^2 + \frac{1}{2} I_{\varphi} \dot{\varphi}^2 - m g R \sin \theta \\ } $$

where $I_{\psi}, I_{\theta}$ and $I_{\varphi}$ are the moments of inertia of the coin about the different axis of rotation.

Constraints:

The system isn't only described by this Lagrangian. We have to apply the conditions of rolling without slipping. Using the transport theorem (where $\mathbf R_c$ is the point of contact of the coin with the floor): $$ \left ( \frac{d \mathbf R_c}{d t} \right)_S = \left ( \frac{d \mathbf R_c}{d t} \right)_{S'} + \boldsymbol \omega \times \mathbf R_c $$ we have that the point of contact, as seen from the coin reference frame, isn't moving so: $$ \left (\frac{d \mathbf R_c}{d t} \right)_{S'} = \mathbf 0 $$ hence: $$ \left ( \frac{d \mathbf R_c}{d t} \right)_S = \boldsymbol \omega \times \mathbf R_c $$

finally we have our non-holonomic constraint equations: $$\begin{pmatrix} \dot{x} - R \dot{\theta} \sin \theta \cos \varphi - R \dot{\varphi} \cos \theta \sin \varphi \\ \dot{y} - R \dot{\theta} \sin \theta \sin\varphi + R \dot{\varphi} \cos \theta \cos \varphi \\ 0 \end{pmatrix} = \begin{pmatrix} - R \dot{\psi} \sin \varphi \\ R \dot{\psi} \cos \varphi \\ 0 \end{pmatrix} $$ applying this to the Lagrangian: $$ \boxed{ \\ \; \\ \mathcal L = \frac{1}{2} m R^2 \left ( \dot{\theta}^2 + \dot{\psi}^2 + \dot{\varphi}^2 \cos^2 \theta - 2 \dot{\varphi} \dot{\psi} \cos \theta \right) + \frac{1}{2} I_{\psi} \dot{\psi}^2 + \frac{1}{2} I_{\theta} \dot{\theta}^2 + \frac{1}{2} I_{\varphi} \dot{\varphi}^2 - m g R \sin \theta \\ } $$

The thing is, are all of these parameters enough? Not only in the sense that this is a simplistic model, but given this simplistic model, are there any other constraints I should apply to get a physical result?

Simulation:

I've tried to simulate the system:

As you can see in the video it seems "physical". The problem is: when spinning the coin around the $\varphi$ axis, I expected a motion similar to an Euler's disk, but the system does some strange motion (probably due to not imposing a constraint on the floor being solid and the center of mass height must be positive). Is this an extra constraint to add, or an Euler's disk description does not need this constrain. What I mean with this is that if a rotating disk height will remain positive without any constraint, or is this constraint needed?

Here it is an example of what I was saying (for the coin to fall we have $\theta(t = 0) = \pi / 2 - \varepsilon$ with $\varepsilon \sim 0$):

It rotates upright a little bit until it falls and starts to perform this strange motion and begins to clip through the floor. This can't be right. What other constraints are needed?

Note: I didn't mention it but $I_\varphi$ depends on $\theta$, because it isn't the same to rotate the disk around $\varphi$ when it lays on the floor, than when it is upright.

Note: I just want to know if this assumptions represent a physical problem, only that.

---

Here it is the code if you want to try the simulation.

Answer 1

The solution was much easier than expected. After trying to update the integration algorithm on the simulation, everything continued to give the same behaviour.

After some time thinking, I realised that maybe $\dot{\varphi}$ was different to the angular velocity on the z axis $\omega_z$ in the global reference frame.

$$ \mathbf x(t) = R(t)\mathbf x(0) $$ $$ \dot{\mathbf x}(t)= \dot{R}(t)\mathbf x(0) $$ Then from the first equation: $$ \dot{\mathbf x}(t)= \dot{R}(t) R^T(t)\mathbf x(t) = \Omega(t) \mathbf x(t) $$ This is equivalent to computing the velocity via: $$ \dot{\mathbf x}(t) = \Omega(t) \mathbf x(t) = \boldsymbol \omega \times \mathbf x(t) $$ Computing the Angular Velocity Matrix: $$ \Omega = \dot{R}(t)R^T(t) $$ and associating it to $\boldsymbol \omega$: $$ \boldsymbol \omega = \begin{pmatrix} \dot{\theta} \sin \varphi - \dot{\psi} \cos \varphi \sin \theta \\ -\dot{\psi} \sin \varphi \sin \theta - \dot{\theta} \cos \varphi \\ \dot{\varphi} + \dot{\psi} \cos \theta \end{pmatrix} $$ Finally: $$ \omega_z = \dot{\varphi} + \dot{\psi} \cos \theta $$ My guess that: $\omega_z = \dot{\varphi}$ was not far from reality, it only needed to be corrected by the new term.

So imagine I want to impose the initial condition: $\omega_z(0)$, $\dot{\varphi}(0)$ goes as follows: $$ \dot{\varphi}(0) = \omega_z(0) - \dot{\psi}(0) \cos \theta(0) $$

Also the rotational kinetic energy must be rewritten in terms of the new angular velocities as seen from the body axis.

---

Final result: