4

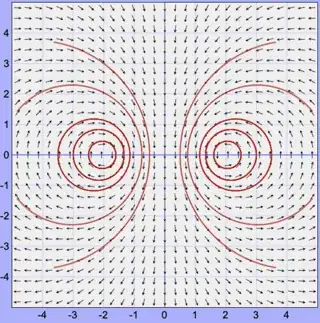
So my fluid's professor gave us an exercise where we had to calculate the force exerted on a wall by a vortex separated a distance $d$ to it. By the method of images we can build the complex potential $$w=i\frac{\Gamma}{2\pi}\log\left(\frac{z+d}{z-d}\right)$$ Taking into account that $\frac{\mathrm{d}w}{\mathrm{d}z}=v_x-iv_y$, the velocity field derived from this potential looks like this:

For this particular case <span class=$d=2$" />

Let's say the wall is at the left ($-\infty<x<0$), and the real vortex is the one at the right (the left vortex exists for the mere purpose of making 0 the $x$ velocity component at $y=0$ to create the effect of the wall, because of the method of images). If we want to know the force exerted on the wall by the vortex on the right we can use Blasius' theorem: $$F_x-iF_y=\frac{i}{2}\rho\oint_C\left(\frac{\mathrm{d} w}{\mathrm{d}z}\right)^2\mathrm{d}z=-\frac{i\rho\Gamma^2d^2}{2\pi^2}\oint_C\frac{\mathrm{d}z}{(z-d)^2(z+d)^2}$$ In theory I have to use a contour that encloses the object. I used a contour which is a semicircle going from $y=-R$ to $y=R$ and then closing in the left completing the semicircle. Then $R\rightarrow \infty$ and the whole wall is enclosed. This is a contour commonly used in complex variable. However, as the goal is not to compute really a real integral over the $y$ axis, I can simply choose a circular contour enclosing just the second order pole at $x=-d$, or any kind of counterclockwise contour that encloses the left vortex. This is stated in Kundu's book:

[...] where $C$ denotes a counterclockwise contour coinciding with the body surface.

[...] any contour surrounding the body can be chosen, provided that there are no singularities between the body and the contour chosen.

Anyways, the main point is that we can calculate the integral as the residue of the function at $z=-d$. In this case, it is $\frac{1}{4d^3}$. Doing so, I obtained: $$F_x-iF_y=-\frac{i\rho\Gamma^2d^2}{2\pi^2}2\pi i \frac{1}{4d^3}=\frac{\Gamma^2\rho}{4\pi d}$$ Now, this result seems to me very unsettling. Just by intuition we know that the wall should suffer a force directed to the left, but instead we obtain a force which points to the right. Also, it also doesn't feel right that there is no net force in the vertical direction. Isn't the vortex trying to "drag" the wall downwards? Shouldn't the wall also feel some net force in the negative $y$ direction?

I'm pretty sure that the calculations for the integral are well done, as my professor and classmates obtained the same result. However, it may be the case that we all got it wrong. So if it isn't the calculation, is it that I haven't correctly applied the theorem? Is something about the contour? Is it that because the contour is infinite now the theorem doen's apply? I'm very confused.

Bob D
  • 81,786
adricello05
  • 117

1 Answers1

2

I'll give show you the application of method of images without relying on complex analysis, that only introduces unnecessary complications if you can't use it properly.

The velocity field can be written as the superposition of the effects of the two vortices as

$$\begin{aligned} \mathbf{u}(x,y) & = -\frac{\Gamma}{2 \pi } \frac{1}{(x-d)^2+y^2} \left[ -y \hat{\mathbf{x}} + + (x-d) \hat{\mathbf{y}} \right]+ \\ & \quad -\frac{\Gamma}{2 \pi } \frac{1}{(x+d)^2+y^2} \left[ -y \hat{\mathbf{x}} + + (x+d) \hat{\mathbf{y}} \right] \ . \end{aligned}$$

Now, let's use Bernoulli's principle

$$P_0 = P(x,y) + \frac{1}{2} \rho |\mathbf{u}(x,y)|^2 $$

to evaluate the pressure on the the plane $x = 0$,

$$\begin{aligned} P(x=0,y) & = P_0 - \dfrac{1}{2} \rho |\mathbf{u}(0,y)|^2 = \\ & = P_0 - \dfrac{1}{2} \dfrac{\rho \Gamma^2}{\pi^2} \dfrac{d^2}{(d^2 + y^2)^2} \\ \end{aligned}$$

Now, you just need to evaluate the integral over the length of the plate,

$$\mathbf{F} = - \int_{a}^{b} P \hat{\mathbf{x}} \, dy $$

$$\begin{aligned} F_x = - \int_{y=a}^{b} P(0,y) \, dy & = \int_{y=a}^{b} \left[ - P_0 + \dfrac{1}{2} \dfrac{\rho \Gamma^2}{\pi^2} \dfrac{d^2}{(d^2 + y^2)^2} \right] \, dy = \\ & = - P_0 (b-a) + \dfrac{1}{2}\dfrac{\rho \Gamma^2}{\pi^2 d} \left[ \dfrac{1}{2} \left( \frac{y/d}{1+\frac{y^2}{d^2}} + \arctan\left( \frac{y}{d} \right) \right)\right]_{y=a}^b \\ \end{aligned}$$

basics
  • 13,368