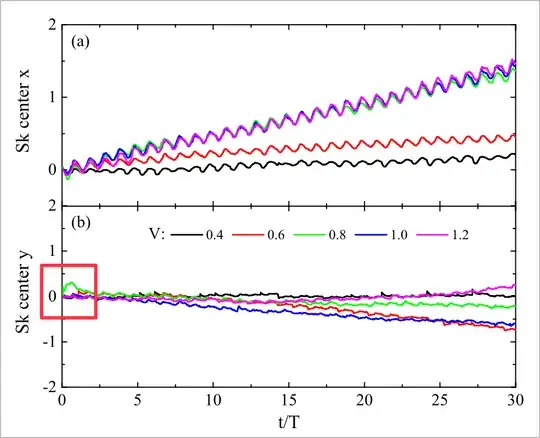
We see that when the system is driven with an oscillating potential ($V\ge 0.8$), the skyrmion initially reacts to the force not only along $\hat x$ but with also transient (Hall-effect like motion) along $\hat y$.
As per the Hall effect (transverse deflection of charged particles due to the Lorentz force), the Skyrmion Hall effect occurs when motion in one direction induces an orthogonal response (y-direction in your diagrams), due to the topological nature of the Skyrmion$^1$.
From the paper:
The well-known Hall effect describes the transverse deflection of charged particles (electrons or holes) in an electric-current carrying conductor under the influence of perpendicular magnetic fields, as a result of the Lorentz force. Similarly, it is intriguing to examine if quasi-particles without an electric charge, but with a topological charge, show related transverse motion. Chiral magnetic skyrmions with a well-defined spin topology resulting in a unit topological charge serve as good candidates to test this hypothesis.
The initial small oscllation in the y-direction when $V\ge 0.8$ is a brief perturbation due to the Skyrmion Hall effect, before it locks into its main path (along the x-direction as per your diagrams). If you wanted to, you could prove this via a computation using the Thiele equation$^2$ (used to describe the dynamics of topological solitons).
You should also note that in the paper you cite, it is stated:
When an electron traverses the Sk, it acquires a Berry phase and experiences a
Lorentz-like force, leading to the topological Hall effect. At the same time, the Magnus force due to the back action on Sk gives rise to Skyrmion Hall effect
$^1$ Although the skyrmion itself is electrically neutral, it has topological charge (see link).
$^2$ The Thiele equation
$$\vec{G} \times \vec{v} - \alpha {\bf D} \cdot \vec{v} + \vec{F}_{\text{ext}} = 0$$ can model the dynamics of a Skyrmion's center of mass ("mass" is used very carefully here as skyrmions are a little more subtle - i.e., "effective mass" is perhaps better) under external forces/potentials.
In this equation, $\vec{v}$ is the velocity of the Skyrmion center of mass, $\vec{G}$ is the gyrocoupling vector, $\alpha$ is the Gilbert damping constant, $\bf D$ is the dissipative tensor (usually taken to be diagonal), i.e., ${\bf D} = D \delta_{ij}$ and $\vec{F}_{\text{ext}}$ is the external force (due to the potential).
So for an external driving force in the $x$-direction:
$$
\vec{F}_{\text{ext}} = (F_x(t), 0)$$
and with $\vec v =(v_x,v_y)$ then a little algebra, we get the two equations
$$
- G v_y - \alpha D v_x + F_x(t) = 0 \\
G v_x - \alpha D v_y = 0$$
Solving these equations for $v_x$ and $v_y$
yields
$$v_x(t) = \frac{F_x(t)}{ \frac{G^2}{\alpha D} + \alpha D } \\
v_y(t) = \frac{G}{\alpha D} v_x(t)$$
Note how the Skyrmion acquires a transverse velocity $v_y$ even though the force applied was strictly in the $\hat x$ direction.