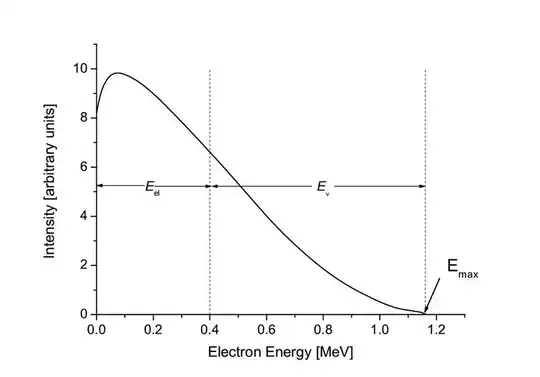
I am confused why beta decay can emit energy. While I know proton decay is impossible because the neutron weighs more than the proton I think we can apply the same logic for other reactions. Consider the reaction:
Carbon 14 mass: 14.003 242 Da
Nitrogen mass: 14.003 074 Da
Electron mass: 0.000 548 Da
Thus the mass of the products is 14.003 622 daltons which is more energy than the reactant and therefore it must absorb energy, right?
The masses you have found are for neutral atoms (which is the standard convention.) But when the decay happens, the electrons that were orbiting the parent atom are unaffected. So what really happens in this decay is $$ \text{(Carbon-14 nucleus & 6 electrons)} \to \text{(Nitrogen-14 nucleus & 6 electrons)} + \text{(one electron)} $$ This means that the daughter nucleus is missing one electron relative to a neutral atom, which would have 7 electrons. There's also one free electron that has been ejected. In other words, the mass of the products is equal to the mass of a neutral nitrogen-14 atom — not the mass of a neutral ${}^{14} \text{N}$ atom plus one electron.
Thus, the mass of the products is less than the mass of the reactant, and the reaction can proceed spontaneously.
What happens in $\beta^-$ decay, is that neutron in carbon nuclei transmutes into proton, hereby converting nuclei into Nitrogen, so in the nuclei there undergoes a reaction, $$n \to p + e^− + \bar ν_e.$$
One of possible decay scenarios is when electron antineutrino carries away residual energy of,
$$ (m_n-m_p−m_e)×c^2 \approx 0.78~\text{MeV}$$ of energy, so that energy conservation would be always satisfied. Hence, the energy output.
EDIT:
But exact energy partition schematics between electron and antineutrino is random :
My example is just one of possibilities of lowest electron kinetic energy and highest of antineutrino. Anyway, they share same mass excess of $m_n-m_p.$
In summary, beta decay generates energy, because neutron $\approx 1.0014\times$ is heavier than proton, and upon transmutation, this mass excess must transfer somewhere.
