Optical or Geometrical length in ABCD Matrix?

Question

I'm trying to obtain the correct expression of the waist of a gaussian beam with respect to the ABCD Matrix coefficients in a bow-tie ring cavity, where one places a non-linear crystal of index $n$ and length $l_c$.

For an homogenous medium of refractive index n, the ray transfer matrix of a free propagation is typically writted as:

\begin{pmatrix}1 & L/n \\ 0 & 1\end{pmatrix}

Another user asked a similar question and got this answer stating $L$ is the geometrical length (I personally don't understand the use of the refraction matrices considering the incidence on the interface is normal).

However, in a paper I found, they take an optical path length instead of the geometrical one:

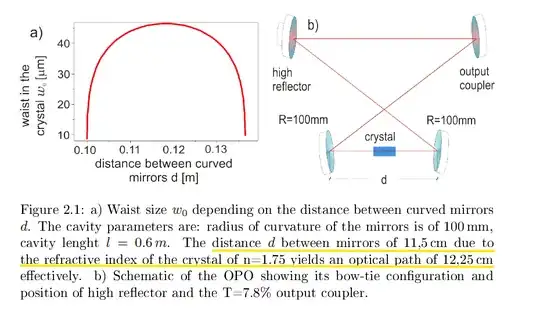
Thus writing the propagation matrix as followed:

My question is, is $L$ in the free space propagation the geometrical length, or did the authors of this article make a mistake?

Answer 1

To find the optical path length $L_o$, you do need to multiply the geometric path length $L_g$ - the thickness of your crystal along the propagation axis - by the refractive index of the material at that wavelength, i.e., $$ L_o = L_g \cdot n $$ So you can effectively replace the transfer matrix of the crystal by an equivalent "air path" matrix that takes into account the refractive index; this holds as long as the displacement of the beam is small due to small angles of incidence, i.e., as long as $\sin \theta \approx \theta$.

So the matrix $$ \begin{pmatrix}1 & L/n \\ 0 & 1\end{pmatrix} $$ is essentially correct. There are some lecture notes from ECE Illinois that elaborate on this topic well.

In bow-tie cavities, however, the faces of the gain medium are often at Brewster angle to extinguish unwanted polarization modes, so the calculation can become more involved. If you want to calculate the ABCD matrix of the whole cavity system easily, I recommend the reZonator software or refer to their index of ABCD matrices, such as for Brewster crystals.