Does applying two successive (orthogonal) boosts contradict Einstein's first postulate of relativity?

Question

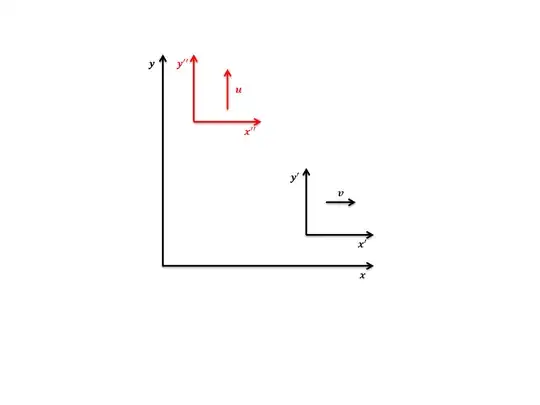
According to the first postulate of relativity, physics laws (formulae) keep their mathematical form from one reference frame to another with a relative velocity, meaning that the following equations can be written in the primed in terms of the unprimed values: [see the figure] $$x'=\gamma_v (x-vt),\space\space y'=y, \space\space t'=\gamma_v (t-vx/c^2)$$ where $\gamma_v=1/\sqrt{1-v^2/c^2}$. Now, if we want to obtain the relevant equations in the unprimed system, and according to the SR first postulate, it suffices to replace any unprimed values with their primed counterpart and vice versa and also change $v$ to $-v$ since the direction of velocity is opposite as measured in each frame. Therefore, we have: $$x=\gamma_v (x'+vt'),\space\space y=y', \space\space t=\gamma_v (t'+vx'/c^2)$$ Now, assume a third frame of reference (double primed system colored red) moving at $u$ along the $y$-axis relative to the unprimed system. It is evident that the following equations are valid: [see the figure] $$x''=x,\space\space y''=\gamma_u (y-ut), \space\space t''=\gamma_u (t-uy/c^2)$$ where $\gamma_u=1/\sqrt{1-u^2/c^2}$. Again, if we want to obtain the relevant equations in the unprimed system, and according to the SR first postulate, it suffices to replace any unprimed values with their double primed counterparts and vice versa and also change $u$ to $-u$ since the direction of velocity is opposite as measured in each frame. Therefore, we have: $$x=x'',\space\space y=\gamma_u (y''+ut''), \space\space t=\gamma_u (t''+uy''/c^2)$$ However, if we decide to connect the primed system to the double primed one by eliminating the unprimed values, we get: $$x'=\gamma_v x''-v\gamma_v \gamma_u (t''+uy''/c^2),\space\space y'=\gamma_u (y''+ut''), \space\space t'=\gamma_v \gamma_u (t''+uy''/c^2)-v\gamma_v x''/c^2$$ According to Einstein's first postulate, we anticipate that the equations in the double primed system can be obtained by replacing the primed values with their double primed counterpart and vice versa and changing $u$ to $-u$ and $v$ to $-v$. However, this is amazingly not the case! Indeed, the equations in the double primed system are as follows: $$x''=\gamma_v (x'+vt'),\space\space y''=\gamma_u y'-u\gamma_v \gamma_u (t'+vx'/c^2), \space\space t''=\gamma_v \gamma_u (t'+vx'/c^2)-u\gamma_u y'/c^2$$ Remember that I know that the result of two successive boosts is not a pure boost but a boost accompanied by a (Wigner) rotation. However, it seems that the two last groups of equations are not in agreement with Einstein's first postulate, meaning that the mathematical forms are not invariant in some cases. Am I not right?!

Update #1: One may say that there is a difference between physical laws and coordinate transformations. It is worth mentioning that $x=vt$ is a simple physical law that indicates the spatial position of a particle (moving at $v$) as time progresses. Now, if this equation does not keep its form from one reference frame to another under any transformation, we can claim that this simple physical law is not invariant, which violates Einstein's first postulate. Otherwise, one should elaborate on what the first postulate exactly means.

Update #2: To defend my approach, I refer the reader to this Wiki article under the sentence First Postulate (Principle of relativity), which very well describes this postulate the same as I did.

I cannot understand the intentions behind this high amount of downvotes and votes to close, while I have both presented a clear question and done correct calculations.

Answer 1

According to Einstein's first postulate, we anticipate that the equations in the double primed system can be obtained by replacing the primed values with their double primed counterpart and vice versa and changing $u$ to $−u$ and $v$ to $−v$.

This is your error. The equations will of course be completely different. The first postulate states that the laws of physics, i.e. the actual dynamics of the interactions between bodies, will be identical between reference frames. The laws can be stated in their simplest form in all frames of reference. This is not contradicted by anything that you wrote.

It is also not the case that the equations for the Lorentz transformations are the same in all circumstances, in fact most of the time they're not. If you superimpose Lorentz transforms on each other like you have, you will of course not get the simple high-school case that is always taught first.

It is worth mentioning that $x=vt$ is a simple physical law.

Also wrong. $x$ and $t$ are coordinates and $v$ is a parameter. As such, the validity of this expression depends entirely on what coordinates you use. For example: if $x$ if the spatial coordinate in frame 1 and $t$ is the temporal coordinate in frame 2, for two different frames 1 and 2, then of course $x=vt$ will likely not maintain between those frames of reference. I can choose arbitrary coordinates; it should make sense, then, that the coordinate-based equations can also be made arbitrarily true or false, depending on that choice.

A physical law is something like $E_m=mc^2$ (disregarding contributions from other sources). All observers will always agree that this rest mass-energy is the same across reference frames; it is a scalar quantity in that sense, as opposed to a vector quantity (like position in space and time, or velocity, or momentum) or tensor quantity (like the electromagnetic tensor) that depends on coordinate systems. Another good scalar is the spacetime interval $\text ds^2$ between two events, which all observers agree on.

You do not need any reference to coordinate systems or such to deal with special relativity. The proper way this is done is with general relativity's abstract index notation, with the normal flat-spacetime setting $g=\eta$, recovering all the properties of special relativity.