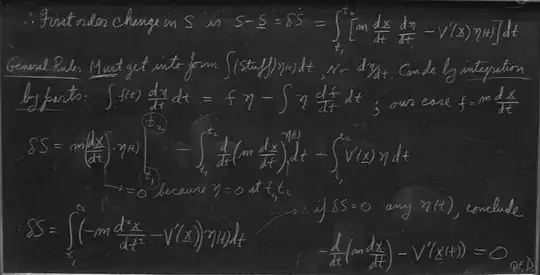Feynman's derivation of Euler-Lagrange equations

Question

From Chapter 19 of Volume 2 of The Feynman Lectures on Physics, the following integral is supposed to be zero for any $\eta(t)$ I choose.

$$\delta S = \int_{t_1}^{t_2}\left[m\frac{d\underline{x}}{dt}\frac{d\eta}{dt}-\eta V'\left(\underline{x}\right)\right]dt.$$ Now the problem is this: Here is a certain integral. I don't know what the $\underline{x}$ is yet, but I do know that no matter what $\eta$ is, this integral must be zero. Well, you think, the only way that that can happen is that what multiplies $\eta$ must be zero. But what about the first term with $d\eta/dt$? Well, after all, if $\eta$ can be anything at all, its derivative is anything also, so you conclude that the coefficient of $d\eta/dt$ must also be zero. That isn't quite right. It isn't quite right because there is a connection between $\eta$ and its derivative; they are not absolutely independent, because $\eta(t)$ must be zero at both $t_1$ and $t_2$.

However, I don’t understand the part about dependence of $\eta(t)$ on $\eta’(t)$. If I specify the height at each point of a function, the derivative is already spoken for right? Isn’t $\eta’(t)$ always dependent on $\eta(t)$ irrespective of whether the end points are fixed or not?

Answer 1

I concur: $\eta(t)/dt$ is dependent on $\eta(t)$ anyway.

Referring to the fact that the additive function $\eta(t)$ must be zero at the end points $t_1$ and $t_2$ is superfluous.

[Later edit: contributor Amit checked against the audio record, and the remark about the end points is not present in the audio record. See the answer by Amit.]

I will first discuss why it is that the process of integration by parts allows the derivation to proceed to its intended goal.

After that I will discuss the reasoning presented by Feynman

The variational equation:

$$ \delta S=\int_{t_1}^{t_2}\biggl[ m\,\frac{d\underline{x}}{dt}\, \frac{d\eta}{dt}-\eta V'(\underline{x}) \biggr]dt \tag{1} $$

In order to bring the variational equation to a form that can be solved two elements must be dismissed: the variational addition $\eta$, and the integration.

Dismissal of the variational addition $\eta$ is expected, of course. For comparison the procedure with differential calculus. Add a small quantity to $x$: ($x + h$), and then work towards a form where you can take the limit of $h$ going to infinitesimally small.

In the case of processing the variational equation: processing it has a dual goal: to allow the variational addition $\eta$ to disappear, and to dismiss the integration.

We have: at the end of the derivation the resulting equation is a differential equation. The reason for transforming to a differential equation: the differential equation is solvable.

In the form as stated above the integration cannot be dismissed, because the expression contains both the function $\eta(t)$ and its time derivative: $d\eta(t)/dt$.

In preparation I formulate a lemma:
As you sweep out variation: the piece of information that you need is the derivative of the action at the point in variation space where the trial trajectory coincides with the true trajectory. Lemma: when two curves coincide they have the same derivative.

The product rule of differentiation:

$$ \frac{d}{dt}(\eta f)= \eta\,\frac{df}{dt} + f\,\frac{d\eta}{dt} \tag{2} $$

In the process of integration by parts the relation expressed by (2) is used to transfer differentiation with respect to time from $\eta(t)$ to $m\,\tfrac{d\underline{x}}{dt}$.

That is, the differentiation with respect to time is not eliminated: it is transferred from $\eta(t)$ to $m\,\tfrac{d\underline{x}}{dt}$.

The statement below outlines the differentiation transfer:

$$ m\,\frac{d\underline{x}}{dt}\,\frac{d\eta}{dt} \quad \Leftrightarrow \quad \frac{d}{dt}\biggl(m\,\frac{d\underline{x}}{dt}\biggr)\eta(t) \tag{3} $$

That raises the question: how is it valid to transfer the differentiation? Well, what is being evaluated is the point in variation space where the trial trajectory coincides with the true trajectory. Same curve, same derivative.

The result:

$$ \delta S=\int_{t_1}^{t_2}\biggl[ -m\,\frac{d^2\underline{x}}{dt^2}-V'(\underline{x}) \biggr]\eta(t)\,dt \tag{4} $$

In the above equation the terms have already been rearranged to have the core expression inside the square brackets, and all auxillary elements outside it.

(4) is at the point where the integration can be dismissed.

Feynman's presentation

Feynman offers the following consideration:

[...] there is a connection between η and its derivative; they are not absolutely independent, [...]

Feynman suggests that there's a problem there, but the very thing that makes it possible to deploy integration by parts is the fact that $d\eta(t)/dt$ and $\eta(t)$ are connected. The integration by parts capitalizes on the are-related-by-differentiation property. The $d\eta(t)/dt$-and-$\eta(t)$-are-connected circumstance isn't a problem, it's an asset.

General discussion

Differential equations form a special category of equation.

Let me contrast differential equations and the type of equation for finding the root(s) of a function. When you solve a root finding equation the solution is one or more numbers. When a differential equation is solved the solution is a function. That is: the solution space of differential equations is a space of functions.

We have: for a differential equation the demand is that the stated differential relation must be satisfied for the whole domain concurrently. That is: the demand expressed by the differential equation is intrinsically a global demand.

Variational equations have that global property too. The solution to a variational equation is a function.

That shared property of being a global type of equation is what makes it possible to transform a variational equation into a differential equation.

About global and local

The following is quoted from the chapter that triggered the question:
Feynman Lectures, Volume II, chapter 19

Note:
I have applied the following change: where it said in the original text 'a minimum' has been replaced with: 'stationary', for the purpose of aligning with the name: Hamilton's stationary action.

"Now I want to say some things on this subject which are similar to the discussions I gave about the principle of least time. There is quite a difference in the characteristic of a law which says a certain integral from one place to another is stationary—which tells something about the whole path—and of a law which says that as you go along, there is a force that makes it accelerate. The second way tells how you inch your way along the path, and the other is a grand statement about the whole path. In the case of light, we talked about the connection of these two. Now, I would like to explain why it is true that there are differential laws when there is a stationary action principle of this kind. The reason is the following: Consider the actual path in space and time. As before, let’s take only one dimension, so we can plot the graph of $x$ as a function of $t$. Along the true path, $S$ is stationary. Let’s suppose that we have the true path and that it goes through some point $a$ in space and time, and also through another nearby point $b$ Now if the entire integral from $t_1$ to $t_2$ is stationary, it is also necessary that the integral along the little section from $a$ to $b$ is also stationary. It can’t be that the part from $a$ to $b$ is a little bit more. Otherwise you could just fiddle with just that piece of the path and make the whole integral fit.
So every subsection of the path must also be stationary. And this is true no matter how short the subsection. Therefore, the principle that the whole path satisfies the stationary criterion can be stated also by saying that an infinitesimal section of path also has a curve such that it has stationary action."

To my knowledge Feynman is the only author to point out the above described property.

(Co-authors Edwin F. Taylor and Jozef Hanc mention it too, stating that they obtained the insight from Feynman's discussion.)

Crucial point:
The validity of the derivation is specifically set up to be independent of where the end points $t_1$ and $t_2$ are positioned.

$t_1$ and $t_2$ do not have to correspond to any particular point along the true trajectory of the physical system.

The whole point is: you can subdivide the trial trajectory any way you want; the validity of the derivation is independent of that.

This includes putting $t_1$ and $t_2$ arbitrarily close together, all the way down to infinitesimally close together; the validity of the derivation stands.

So you put $t_1$ and $t_2$ infinitesimally close together, with the demand that this infinitesimal criterion of stationary action must be satisfied for the whole domain concurrently.

The true trajectory satisfies the stationary action criterion on every infinitesimal subsection of the trajectory: that property propagates out to the trajectory as a whole.

Key:
The trajectory as a whole satisfies the stationary action criterion if and only if it is satisfied on each infinitisimal subjection of the trajectory concurrently.

Answer 2

The phrase in question was added by the authors of FLP (of which there are three, Feynman, Leighton and Sands) to clarify, in the given context, the nature of the “connection” between the deviation [η] and its derivative [dη/dt] to which Feynman refers. This was intended as a segue between the text immediately preceding it, in which Feynman is talking about the unfortunate presence of this derivative in the variation of the action [δS] — in this case a factor in the first term — and the text that immediately follows it, in which this derivative is eliminated in a particular way that is characteristic of the methodology employed in the calculus of variations, so that the variation can be rewritten, through integration by parts, as a product of the deviation and some function, and the solution can then be found by setting that function to zero. (As Feynman puts it, “It turns out that the whole trick of the calculus of variations consists of writing down the variation of [the action] and then integrating by parts so that the derivatives of [the deviation] disappear.”) This is only possible when the deviation is zero at the endpoints of the path, which, of course, they always must be in this context.

So, to summarize (quoting the book): The “connection between [the deviation] and its derivative,” and the reason that the they are “not absolutely independent, because [the deviation] must be zero at both [endpoints of the path]” is because the latter enables “integrating by parts so that the derivatives of [the deviation] disappear.”

This is also reflected on Feynman’s blackboard:

Feynman repeats this point several times in different parts of his lecture, as you can hear in the recording, for example when he is talking about electrodynamics.

These are the facts in this matter. The only postings here that in any way reflect the facts are Lee Mosher’s comment (unsurprisingly, Mosher is a Distinguished Professor of Mathematics at Rutgers University), and to a lesser extent the answers given by Rodrigo de Azevedo, and Jean Daviau. On the other hand, the speculation reflected in various answers and comments posted here, that the presence of this phrase is an error penned by a blundering editor, is without any basis and it is incorrect. That the phrase in question has anything to do with the endpoints of the path being close together is also incorrect.

One can not conclude from the fact that Feynman did not say this when he gave the lecture that he or one of his co-authors did not add it later, which is the case here. In fact you can find many differences between the recording and the written lecture - all made by the authors - and that is why it is introduced as “A special lecture - almost verbatim.”

The claim that the phrase is confusing is, of course, subjective, but apparently it did not confuse Dr. Mosher. Personally I do not find it confusing, nor do my colleagues, nor did the many Caltech professors who used FLP as a textbook or their multitudinous students, so far as I am aware, and I could say the same of the professors and students at The University of Twente, where FLP Volume II has been used as the introductory E&M textbook since the 1960s. At least no one has written to me that there is anything wrong with this phrase in the 25 years I have been editing FLP, until I received an email from one of the posters here who brought my attention to this discussion on Physics Forum.

I will mention in closing that since the first printing of the New Millennium Edition in 2010, many errors have been corrected in this chapter of FLP, mostly numerical and typographical, and a couple (very minor) mathematical, though none in the text, such as that purported in this discussion.

(I think it is highly likely that the reviewers will delete this answer, despite it being the only one that is well-informed. My answers on Stack Exchange usually get deleted. But in any case, I can guarantee that the phrase in question is not going to be changed in FLP because of some speculations posted about it in a public forum.)

Michael A. Gottlieb, Editor, The Feynman Lectures on Physics New Millennium Edition

www.feynmanlectures.caltech.edu

Answer 3

It sounds like he is referring to the fundamental lemma of the calculus of variations:

If $t_2>t_1$ are constants, $G(t)$ is a particular continuous function on $t_1\leq t\leq t_2$ and \begin{equation} \int_{t_1}^{t_2}\eta(t)G(t)=0\tag{1} \end{equation} for every choice of continuously differentiable $\eta(t)$ for which $\eta(t_1)=\eta(t_2)=0$, then \begin{equation} G(t)=0\quad \text{identically on}\quad t_1\leq t\leq t_2.\tag{2} \end{equation}

Its proof requires that there exist at least one $\eta$ such that $(1)$ does not hold, when $(2)$ does not. If there is a particular value of $G$ that is nonzero, say $G(t')>0$, then we can construct $\eta(t)=(t-t_1')^2(t-t_2')^2$ on the interval $(t_1',t_2')$ containing $t'$ with $\eta(t)=0$ outside this interval. $G$ is positive on some $(t_1',t_2')$ by continuity. So, the integral $(1)$ would be positive and we arrive at a contradiction. Similar reasoning applies for the $G(t')<0$ case.

The lemma does not directly apply to $\int_{t_1\leq t\leq t_2}(\eta'(t)G_2(t)+\eta(t)G_1(t))=0$ and so we'd have to integrate by parts and get $G_2'=G_1$ (maybe Feynman is referring to the proof of this statement?).

I am not entirely sure what Feynman means by "connection between $\eta$ and its derivative". I suppose a Taylor expansion gives $\eta(t)=\eta(t_1)+(t-t_1)\eta'(t_1)+....=(t-t_1)\eta'(t_1)$ in a neighbourhood of $t=t_1$ and would "connect" $\eta$ and $\eta'$ at that point.

Answer 4

I think Feynman may have been alluding to an analogy between this and the way we define linear independence of vectors in a vector space.

One way to say a pair of vectors is independent is:

$$ c_1\vec{v}_1 + c_2\vec{v}_2 = 0 \ \text{ iff }\ c_1=c_2=0 $$

But here, if we take $\vec{v}_1=\eta$ and $\vec{v}_2=\dot{\eta}$, they're not independent, so $c_1,c_2$ may be nonzero and yet due to the linear dependence, the combination $c_1\vec{v}_1 + c_2\vec{v}_2$ may vanish. For example, consider $\vec{v}_1=\eta(t)=kt$, so $\vec{v}_2=\dot{\eta}=k$. Clearly we can pick $c_1=1, c_2=-t$ and find:

$$ c_1\vec{v}_1 + c_2\vec{v}_2 = \eta - t\dot{\eta} = kt - kt = 0,$$

where we have clearly exploited the relation of $\eta$ and $\dot{\eta}$ to choose the nonzero coefficients $c_1$ and $c_2$.

Incidentally, it may appear weird to you that I'm talking about a vector space where the scalars themselves are also functions. That's because it isn't, strictly speaking a vector space. Formally this is a module over continuously differentiable functions in $\mathbb{R}$.

---

Addendum

Regarding the specific doubt you mentioned here:

Isn't $\eta'(t)$ always dependent on $\eta(t)$ irrespective of whether the end points are fixed or not?

As noted already in the answer provided by Cleonis, you are indeed correct. The interesting fact I found later is that Feynman actually never added the part written "because $\eta(t)$ must be zero at both $t_1$ and $t_2$". This is apparently an editorial addition which in this case is quite confusing. The fact that $\eta(t)$ vanishes at the endpoints is important a bit later, when we use integration by parts, but that's completely unrelated to the dependence of $\eta$ on its derivative, which indeed always holds.

I'll add here my own transcription of Feynman's actual words from the audio which can be accessed here, by clicking on the left hand pane, and then on the recording tape shaped icon. The relevant part is at ~17:55,

[...] Now the game is this, problem: here is a certain integral. I don't know what the $\underline{x}$ is yet, but I know this: that no matter what $\eta$ is, this integral must be zero. No matter what $\eta$ is. You think oh, the only way that can happen is that the thing that's in front of the $\eta$ must be zero. But what about this? [referring to the second term probably] well, after all if $\eta$ is anything, its derivative can be anything also, so you conclude that both of these [coefficients] must be zero. That isn't quite right. That isn't quite right, because there's a connection between $\eta$ and its derivative and they're not absolutely independent. The method of solving all of these problems [...]

The start of the part I have written in emphasis is where the remark about the endpoints was inserted. So for what it's worth, another lesson to learn here is that it can be useful to listen to the audio in conjunction with these lectures if you can, that in itself can give you a better sense of what Feynman was really trying to put across, and in this case, also help you avoid tripping over an editorial blunder.

Answer 5

Integrating by parts and assuming that $\eta (t_1) = \eta (t_2) = 0$, one can "remove" the pesky $\dot \eta$ as follows.

$$ \begin{aligned} \delta S &= \int_{t_1}^{t_2} \left( m \, \dot{\bar x} (t) \, {\dot \eta} (t) - \eta (t) \, V'({\bar x}(t)) \right) {\rm d} t \\ &= \underbrace{\left( m \, \dot{\bar x} (t) \, \eta (t) \, \Big|_{t_1}^{t_2} \right)}_{=0 \text{ because } \eta (t_1) = \eta (t_2) = 0} + \int_{t_1}^{t_2} \left(- m \, \ddot{\bar x} (t) - \, V'({\bar x}(t)) \right) \eta (t) \, {\rm d} t = \color{blue}{\left\langle - m \, \ddot{\bar x} - V'({\bar x}), \eta \right\rangle_{[t_1, t_2]}} \end{aligned} $$

which is an infinite-dimensional inner product, namely, the inner product of the functional gradient $- m \ddot{\bar x} - V'({\bar x})$ and an arbitrary function $\eta$ with $\eta (t_1) = \eta (t_2) = 0$. This infinite-dimensional inner product is the infinite-dimensional directional derivative of the Lagrangian in the "direction" of $\eta$ at $\bar{x}$. If

$$\delta S = \left\langle - m \, \ddot{\bar x} - V'({\bar x}), \eta \right\rangle_{[t_1, t_2]} = 0$$

for all $\eta$, then the functional gradient has vanished and, thus, $m \, \ddot{\bar x} = - V'({\bar x})$, i.e., along the critical path $\bar x$, the force is the negated gradient of the potential $V$.

---

_{Reminder! In the finite-dimensional case, the directional derivative of a differentiable scalar field $f : {\Bbb R}^n \to {\Bbb R}$ in the direction of vector $\bf v$ at point $\bar{\bf x}$ is given by the (finite-dimensional) inner product $\langle \nabla f(\bar{\bf x}), {\bf v} \rangle$. Thus, if $\langle \nabla f(\bar{\bf x}), {\bf v} \rangle = 0$ for all ${\bf v} \in {\Bbb R}^n$, then $\nabla f(\bar{\bf x}) = {\bf 0}_n$, i.e., $\bar{\bf x}$ is a critical point. Why? Because the only vector that is orthogonal to all vectors in ${\Bbb R}^n$ is the zero vector ${\bf 0}_n$.}