1

We have to assume the internal forces to be central (and also assume newton's third law to be true) to prove the equation $\tau=\frac{d L}{dt}$ for a system of particles ,where $\tau$ is net torque on system due to external forces only ( Net torque due to internal forces sums out to be zero if those assumptions hold true) and $L$ is net angular momentum of system .

But centrality of internal forces does not makes sense in some cases of dynamics of planar and one dimensional rigid bodies.
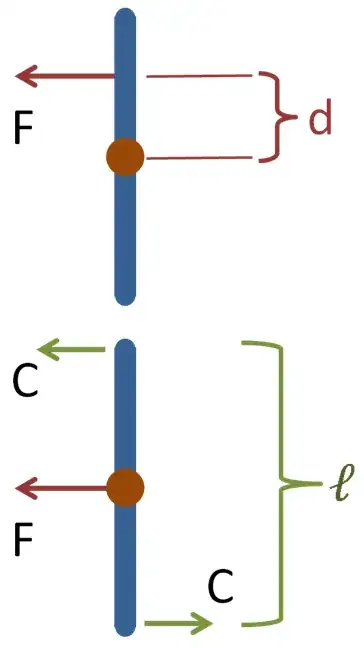
To give a simple example, Let there are two particles at a distance rigidly attached to each other by a one dimensional rod. Let the center of this rod be fixed. Now, apply some force perpendicular to the rod at one of the particles. The rod will start rotating and so can be easily shown by the equation $\tau=\frac{d L}{dt}$ (by considering origin to be at center of rod). But if we consider the dynamics of the particle at the other end separately, it was at rest and after a force was applied on the other particle, it acquires some velocity perpendicular to the rod, which means some force acted on this particle in the same direction, but we assumed internal forces to be central and thus force can act on this particle along the rod only. Similar cases can also be developed when we consider planar rigid bodies. Am I missing something silly?

Edit: So I was going through Chapter 8 (Rigid Body Motion) of An Introduction to Mechanics by Kleppner and Kolenkow and they have explicitly stated in section 8.5 that Conservation of Angular Momentum is an Independent physical law

Newtonian physics is incapable of predicting conservation of angular momentum but no isolated system has yet been encountered experimentally for which the total angular momentum is not conserved. We conclude that conservation of angular momentum is an independent physical law, and until a contradiction is discovered, our physical understanding must be guided by it.

and also discussed an example where internal forces are non-central yet angular momentum of system is conserved. Therefore, my doubt is resolved.

Anmol Singh
  • 33

1 Answers1

0

Since the center of the rod is fixed, the net external force on it is zero. So in this case you have only a net torque but no net external force acting on the system.

Another way to see it is through the concept of Couples. To quote the Wikipedia page:

A force F applied to a rigid body at a distance d from the center of mass has the same effect as the same force applied directly to the center of mass and a couple Cℓ = Fd

In your case, the center of mass is fixed so we are only left with the couple.

Brews ohare, CC BY-SA 3.0 https://creativecommons.org/licenses/by-sa/3.0, via Wikimedia Commons

As the above image should make clear, it is always possible to replace a force with a pair of equal forces that act in opposite directions, and an additional single force acting on the center of mass. This makes it plain that the net force on the center of mass can be zero but the net torque generally need not be. Therefore there is no internal non-central force acting in the scenario you're asking about.

Amit
  • 6,024