Feynman thought experiment for gravitational time dilation

Question

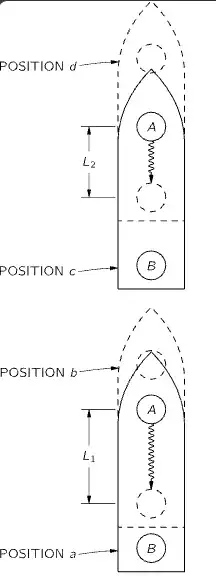
In section 42-6 of The Feynman Lectures on Physics (The speed of clocks in a gravitational field), Feynman describes a thought experiment involving two clocks placed at different positions inside an accelerating rocket. He concludes from an external reference frame that the light traveling from the top clock to the bottom clock covers shorter and shorter distances as the rocket continues to accelerate, indicating that the lower clock (clock B) runs slower.

My confusion is as follows: This conclusion is drawn from an external, inertial observer's perspective outside the rocket. However, from the viewpoint of someone inside the rocket (a non-inertial, accelerating reference frame), the distance between the two clocks remains constant. How can Feynman use observations made from an external inertial frame to infer that the lower clock inside the rocket truly runs slower? Doesn't the observer inside the rocket always measure the same distance and, presumably, the same speed of light?

In other words, how does observing shorter travel distances for the light from an external frame justify concluding time dilation inside the accelerating rocket, when the internal observer sees no change in distance or speed of light?

Answer 1

It is a recurring thing in relativity, that the same phenomenon is given a different description in different reference frames, with the end result and measurements being the same.

Here, I believe the piece that can help you understand what's happening in the rest frame of the ship is related to Bell's spaceship paradox.

To be brief: the paradox imagines two ships tied together by a string, accelerating at the same rate as observed from an outside frame. The question arises, will the string break, due to Lorentz contraction according to an outside observer? If so, what is the corresponding interpretation for observers within the spaceships, and how can they keep that from happening?

It turns out that if we require the acceleration measured from the outside, to be equal for both ships, the back spaceship will measure the proper distance to the leading ship as increasing. The resolution to the paradox then is actually to use an acceleration profile where the front spaceship is accelerating with a smaller proper acceleration. This allows the proper distance between the ships to remain constant, but for an outside observer, the spaceships will appear to be getting closer and closer. He will interpret that as Lorentz contraction, but the string will not break.

This also should give you the answer to your question: the nose of the (single) spaceship must be accelerating at a slower rate than the back, in order for it to hold true that indeed as you said, the proper length between clocks is constant.

Then, a person with the clock at the bottom can physically confirm via an accelerometer that his proper acceleration is greater than that of a person next to the upper clock. The clock at the bottom is "rushing" towards the light pulse faster and faster, corresponding to the "shorter and shorter" distances as seen covered by an outside frame by which Feynman is analyzing the situation. The bottom clock will also receive the light pulses as blue shifted for the same reason.

Answer 2

The ppl inside the rocket see a stationary everything, with the clock in the front ticking faster than the clock near the engines.

That's it.

If the acceleration is $g$, and the length of the rocket is $L$, then the time dilations goes as:

$$ \gamma = \frac{1}{\sqrt{1-\frac{2U}{mc^2}}} $$

with

$$ U = mgL $$

Looks familiar, as in sub in Newtonian kinetic energy:

$$ T = \frac 1 2 m v^2 $$

Answer 3

The clocks run at the same rate. The observer in the rocket sees them running at different rates.

(As there is no relativity in the Feynman's thought experiment, the clocks run at the same rate according to the inertial observer. See the maths, is there any gammas there? No. So there is no relativity)

Feynman ignores length contraction, in other words he makes the simplifying assumption that the clocks move at the same velocity. At high speeds that would be wrong.

About the speed of light in an accelerating rocket:

Said speed is c in a horizontal optical fibre connecting point A and point B. If instead light is sent ballistically from point A to point B then the transmission is quicker and the distance is larger, so speed is higher. Light chooses the path of least time. And the path is a curve in an accelerating rocket.

Rocket starts from rest. After the nose of the rocket has rushed forwards for 100 minutes at acceleration 1 g, a light pulse is sent from the nose towards the floor. When the light hits the floor, the floor has rushed forwards for 100 minutes plus one microsecond at acceleration 1 g plus one femto g. In this case the large time difference is much more important that the small difference of acceleration.

Answer 4

According to Feynman, if clock A sends a light pulse once per second, then clock B will receive a light pulse at intervals slightly shorter than a second. This is used to conclude that clock B is running more slowly. The only part of this argument that depends on the external inertial observer is the prediction that clock B receives light pulses at shorter intervals than clock A sends them. So your question is: would an observer sitting in the rocket not predict that clock B receives the light pulses at the same interval at which clock A sends them?

However, it's important to keep in mind that the purpose of the thought experiment is to reach a conclusion about the laws of physics in accelerated frames when we begin with only knowledge about the laws of physics in inertial frames. In other words, you must start with the assumption that we don't actually know how to predict the amount of elapsed time for clock A and clock B from the point of view of a passenger in the rocket.

But if you actually do analyze the scenario from the passenger's point of view, using everything we actually know about physics, the passenger perceives the universe as being filled with a uniform gravitational field (pointing away from the head of the rocket and toward the tail), which explains why the rocket is apparently standing still while burning fuel, while everything outside the rocket appears to be accelerating. Therefore, the passenger predicts that clock B runs more slowly than clock A, since clock B is deeper in the gravitational well (i.e. it's subject to gravitational time dilation relative to clock A).