We know that a rainbow results from refraction of light, through the air/water interface.
But its arc is narrow, relative to the sky. My question is, what limits the width to such a tight band? On a humid rainy day, shouldn't the entire sky be a rainbow?
For the formation of rainbows and other things relating to rainbows look on this site.
Approximately parallel light from the Sun is refracted and reflected by raindrops and then enters your eye at different angles as shown below.
.
For the primary rainbow with the sunlight only suffering one reflection the predominately red light comes in at an angle of approximately $2^\circ$ above the predominantly blue light and so the angular width of a rainbow is approximately $2^\circ$.
Compare this with the $0.5^\circ$ angular width of the Sun and Moon.
A secondary rainbow is the result of two reflection within the raindrops.
It has a width approximately twice that of a primary rainbow and the colours are inverted.
On a humid rainy day, shouldn't the entire sky be a rainbow?
No, as only raindrops within a fairly defined range reflect direct light from the Sun into your eye as shown in the diagrams above.
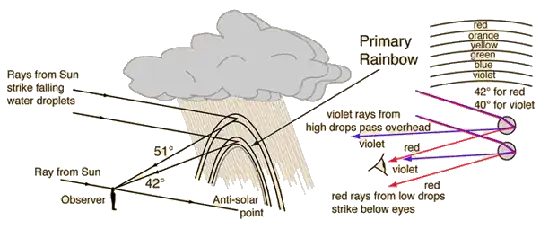
While I stand by my original comment on the question that Veritasium's video is probably all one needs to watch to understand the underlying concepts, underlying concepts aren't the same as actually deriving the result. So I'll walk through the argument of how rainbows work and in so doing answer the question.
Most descriptions of rainbows just say something along the lines of:
Light diffracts when it enters a raindrop, then it reflects on the back of the raindrop, then it diffracts again when it exits the raindrop. In total, the light is deflected by a certain angle, and because refraction is involved in generating that angle, and because the index of refraction depends on wavelength, light of different wavelengths is deflected by different amounts.
There are additional details about how the light from many raindrops is added together, which I will assume the reader understands already - my discussion will not change that part of the argument. I understand that such descriptions are (usually) intentionally simplifying the physics of a rainbow. Often this explanation is provided to children, and I am in no way suggesting that kids should be forced to hear a lecture about caustics.
However, in answering this particular question, I think this description is just totally wrong. It would seem to imply that the rainbow is created for more or less the same reason as a prism spreads light, but this ignores a critical aspect of how rainbows work - light is not deflected in a raindrop by a fixed angle like it is in a triangular prism. The angle depends on the position of the light entering the ray. The rainbow is created by more light being deflected at a particular angle due to an extremum in the deflection angle versus impact parameter:
Consider a beam of light coming into a spherical raindrop at impact parameter $b$. It is ultimately deflected by an angle $\theta$. $\theta$ is a function of $b$, and in fact it turns out that $\theta$ has a maximum deflection angle at a certain impact parameter (which is pretty close to the top of the raindrop). Because the angle depends very weakly on the impact parameter near the maximum, light is concentrated at that angle, making a bright spot called a "caustic." Because refraction is involved in generating the deflection angle, the angle of the caustic depends on the wavelength of the light, and that's what sets the width of the rainbow.
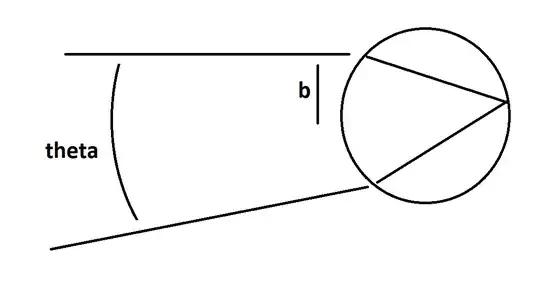Unfortunately, this is a complicated situation, so in order to get at the width of the rainbow, as far as I can tell, the algebra is way too ugly and I'd prefer to use code. So I begin by setting up some python code that can plot how light rays are deflected as a function of $b$ and $n$. An example output is here (you can see where the deflection angle reverses at extreme impact parameter):
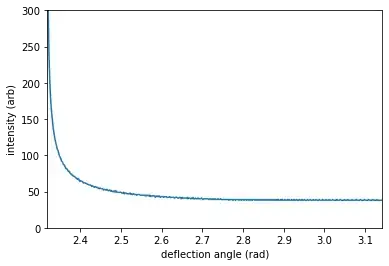
Next, I plot how this deflection angle depends on $n$ and $b$:
Those who believe the "traditional explanation" of rainbows (without the concentration of light due to the angle minimum), might be surprised to know that the majority of the red light (for example) is not deflected by close to 42 degrees to participate in the rainbow. Instead as shown below, the distribution of deflection angles is totally continuous, and it just has a spike near 42 degrees because of the minimum in deflection angle versus impact parameter. So why isn't there a visible rainbow below 42 degrees? Well because all the colors are inside that cone, and they pretty much add up to a constant white light except at the edge of the rainbow. So I would contend that a "rainbow" should be imagined as a cone of white light that ends with a colorful pattern due to each color being concentrated at, and terminating at, a different angle.
Next, I plot how the deflection angle minimum depends on $n$:
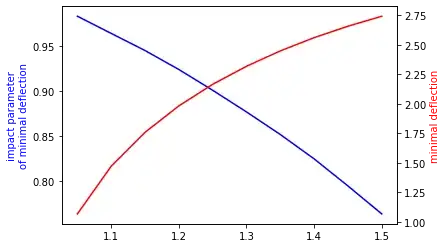
This is what sets the angular width of the rainbow. You take the deflection angle minimum for the index of refraction of water at the minimum wavelength of visible light minus the equivalent quantity for the maximum wavelength of visible light. I found these indeces of refraction to be oddly hard to find; this is the best plot I could find (from philiplaven.com/p20.html, presumably the blog of some person named Philip Laven):
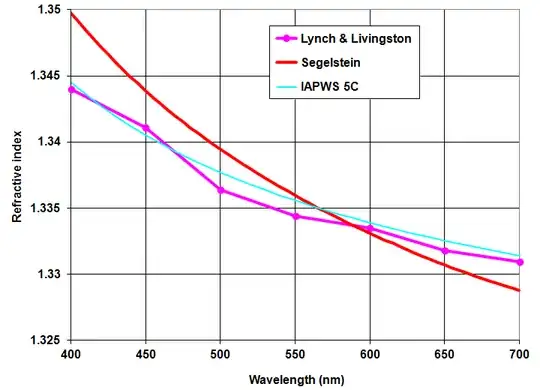
So now let me zoom in on my plot between $n=1.332$ and $n=1.344$:
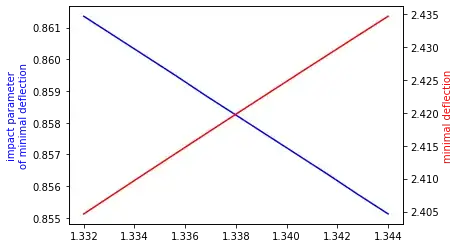
The minimum deflection angles are all around $2.420$ radians, so the opening angle of a rainbow is $\pi-2.420$ radians, or $41.3$ degrees. The difference between the max and min of visible light is $0.03$ radians, or $1.72$ degrees
