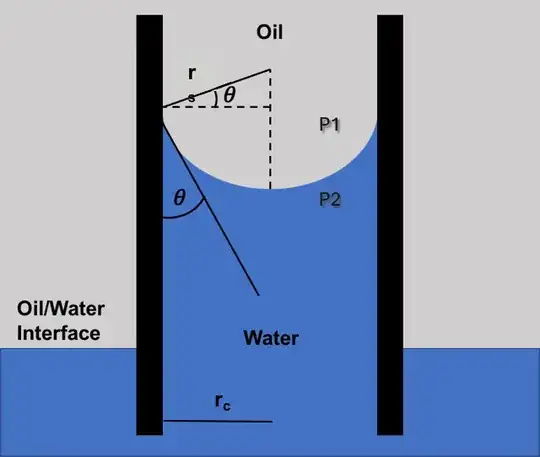
I am facing trouble in understanding how the liquid is even rising
Broadly:
It costs energy to increase surface area because the bonds at a surface are poorly satisfied relative to the bulk. This cost is quantified by the surface tension/surface energy, measured in J/m² (or, equivalently, N/m).
It costs energy to raise the height of a liquid.
Some surfaces—hydrophilic surfaces—bond better to water than to air. The diagram indicates that the inside of the capillary is one such surface. This bonding results in an energy benefit.
Processes occur if the energy benefits pay for the associated costs. Equilibrium corresponds to a balance between the two, such that any change would incur a net energy penalty.
Given all this, we can conclude that the water climbs to wet the inside of the capillary even though it has to rise somewhat. The characteristic meniscus shape arises because it minimizes the total energy of the water surface, the capillary surface, and the gravitational potential energy of the water.
if there the pressure p1 is due to the atmosphere and the pressure at the level of water in the rest of the vessel is also atmospheric i.e P1 then it would lead to a false argument that at the base of the capillary, the pressure should be equal to p1+pressure due to the height of the column on the other hand as it is the same level as the rest of the vessel it would be only p1 I.e atmospheric pressure
Agreed. The pressure at any horizontal level of connected water must be equal. Also, the water pressure at the outer surface level is atmospheric pressure, which we can show with a free-body diagram and force balance. Further, the water pressure must vary with height according to its weight, as you note. The implication is that P2 at the inner surface level must be lower than atmospheric pressure P1. We can interpret this as cohesion between the water molecules as producing a tension or negative gauge pressure. We can also represent this by a surface tension force σ pulling along the water's curved surface:
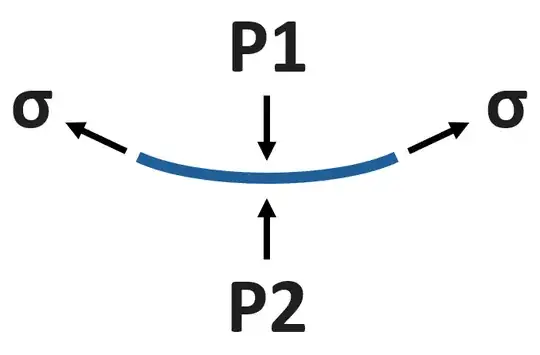
(The surface element is assumed to have infinitesimal thickness, so its weight is negligible. With positive $\sigma$, a vertical force balance yields P2 < P1.)
Am I missing out on any pressure? I know I am missing out on pressure due to surface tension
In general, the pressure on the concave side of a curved liquid surface is always higher, with the difference sometimes termed the Laplace pressure. It arises because liquids tend to rearrange/flow to produce a net energy benefit as described in the bullet points above.