I am trying to understand the derivation of the torque equation
$ \vec{r} \times \vec{F} = I \alpha $
In my book, it is derived easily using Newton's second law for a single point mass $ m $ at a distance $ r $ from the axis of rotation, where the force is applied at the same distance $ r $. The derivation proceeds as follows:
$ F = ma = m (r \alpha) $
Thus,
$ Fr = m r^2 \alpha = I \alpha $
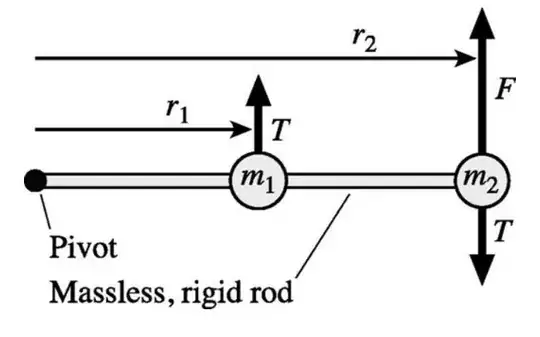
The book stops at this point and concludes that the equation holds for any rotating body. However, when I tried to apply this derivation to a system consisting of two masses positioned on a massless rigid rod, rotating around a fixed axis Let's assume we have two masses, $ m_1 $ and $ m_2 $, at distances $ r_1 $ and $ r_2 $, respectively, with the force applied at $ r_2 $ (as shown in this figure):
Using the same approach, I obtained:
$ F = m_1 a_1 + m_2 a_2 = m_1 r_1 \alpha + m_2 r_2 \alpha $
Thus,
$ r_2 F = (m_1 r_1 r_2 + m_2 r_2^2) \alpha $
However, $ m_1 r_1 r_2 + m_2 r_2^2 $ is not the correct expression for the moment of inertia $ I $ in this case.
I found an article related to this issue at this link :https://pubs.aip.org/aapt/ajp/article/84/2/146/1057171/Comment-on-The-physical-origin-of-torque-and-of
, where the author responds to another paper and critiques it by proposing a model that addresses the same problem I encountered in the textbook.
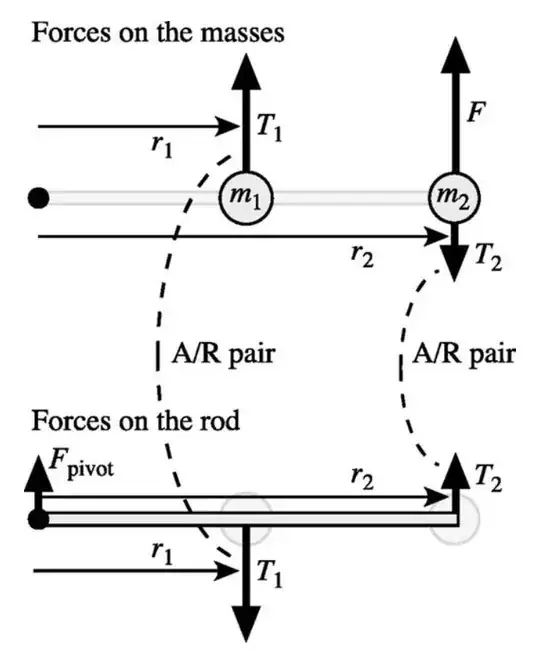
The author first states that the fundamental error arises from a misunderstanding of the applied forces and a misinterpretation of Newton's third law. He explains that the two masses do not interact directly with each other but rather with the rod, which transmits forces between them. He also emphasizes that the tangential forces on the masses cannot be equal in magnitude, as this would result in a net torque on the rod, which is impossible since the rod is massless.
To clarify this, the author compares the situation to a massless rigid rod connected to two masses as shown in this figure
, explaining that there should be no net torque or net force on the rod. Using this principle, he arrives at the following relationship, which ensures zero net torque:
$ r_1 T_1 = r_2 T_2 $
He states that this relationship can be derived directly from Newton's second law for translational motion, without requiring a prior definition of torque. Instead, it can serve as a justification for the commonly accepted definition of torque.
However, this confuses me because I cannot see how this relationship can be derived directly from Newton's second law of translational motion. Could you help me understand the reasoning that leads to this conclusion?