Edit: Ok, I don't understand how this counts as a 'check my work' question given that there is clearly a conceptual error here that I am not getting at. If my purpose was only to find out how to solve this specific form of questions reliably, I'd already have that. In my opinion having the full context behind the source of one's doubt about a concept is more helpful for clarification purposes, but it seems that a line is drawn somewhere. Regardless, here's TLDR of my question (a similar question for reference, apparently closed for the opposite reason):
I came across some difficulties while trying to solve a problem that involves rolling with slipping:
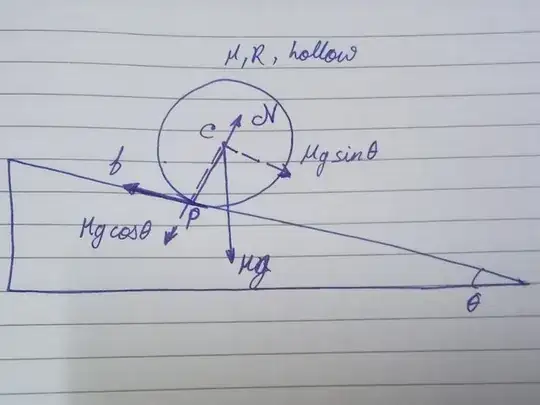
Here is the free body diagram that I constructed for the sphere:
Now, taking torques about P and C and equating angular acceleration $\alpha$, I can solve for $\mu$ that is, coincidentally or not, the same as the minimum coefficient of friction needed to sustain pure rolling:
$$ \alpha = \frac{MgR\sin\theta}{I_P} = \frac{(f = \mu\mathcal{N})R}{I_C} $$ $$ \implies \frac{3g\sin\theta}{5R} = \frac{3\mu Mg\cos\theta}{2MR^2} $$ $$ \implies \mu = \frac{2}{5}\tan\theta $$
As far as I can discern, this does not involve the assumption of pure rolling (?) Now, halving $\mu$ for part (b), the value of $\alpha$ that can be determined from taking torques about $P$ and $C$ do not match, violating the fact that the sphere is rigid. I'm probably missing forces or misinterpreting the changes in forces that arise from going from (a) to (b). What gives?
Edit 2: Ok, so what I am getting here is that I had a misconception about when $\tau = I\alpha$ even applies. As far as I can tell, the reason why $\alpha$ can be taken about the point of contact in rolling without slipping is that the point acts an instantaneous axis of rotation as by definition(?), its velocity is zero with respect to the surface. If angular acceleration about the COM is $\alpha$, it must be $\alpha$ from the frame of reference of the point of contact.
Now when slipping is introduced, my assumption that the point of contact is an instantaneous axis is violated, and so acceleration of points in the body relative to it no longer remains a function of just relative displacement. Again, when equating the two results for angular acceleration about the point of contact, I was implicitly assuming it to be a centre of rotation, and that allowed me to determine the force due to friction, and from there $\mu_{min}$. Am I being correct?