4

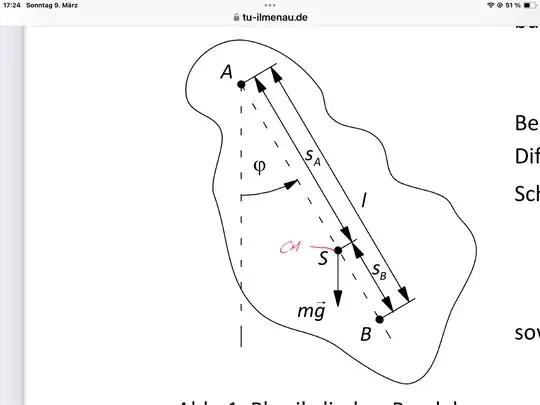
Kater's Pendulum, as explained for example here, is a compound pendulum that can be reversed and the period measured from either side's pivot. If a sliding mass is adjusted so that the two periods are the same, then it is stated that the period is the same as that of the simple pendulum:

$$T = 2\pi\sqrt{\ell/g}$$

where $\ell$ is the distance between the pivots. This is advantageous because the center of mass and the moment of inertia do not need to be determined.

However I must be misunderstanding something. Consider a uniform rod with pivots at exactly its two ends. In such a case the period about each pivot will be the same, and so we should be able to use the above formula, where $\ell$ is the rod's length. But we know such a formula would be incorrect, because it is a well-known result that for a uniform rod:

$$T = 2\pi\sqrt{I/mgr_{cm}} = 2\pi\sqrt{\frac{2}{3}\ell/g}.$$

Therefore the commonly-stated description of Kater's reversible pendulum, as behaving as a simple pendulum with $\ell$ the distance between equal-period pivots, cannot be correct. What am I missing?

Qmechanic
  • 220,844
user1247
  • 7,509

2 Answers2

2

The standard method for determining $g$ via Kater's pendulum requires that the distances between each knife edge and the center of mass are different. To see this, let $I_{CM}$ be the moment of inertia of the pendulum about its CM, and let $l_1$ & $l_2$ be the distances between the CM and the knife edges. The periods of oscillation about each of the knife edges will be $$ T_1 = 2 \pi \sqrt{ \frac{ I_{CM} + M l_1^2}{M g l_1} } \quad \text{ and} \quad T_2 = 2 \pi \sqrt{ \frac{ I_{CM} + M l_2^2}{M g l_2} }. $$ These two periods will be equal if $$ \frac{ I_{CM} + M l_1^2}{l_1} = \frac{ I_{CM} + M l_2^2}{l_2} \quad \Rightarrow \quad I_{CM} (l_2 - l_1) = M l_1 l_2 (l_2 - l_1) $$ There are two ways to satisfy this:

  • Either $I_{CM} = M l_1 l_2$, in which case $T_1 = T_2 = 2 \pi \sqrt{(l_1 + l_2)/g}$. This is the standard result.
  • Or we have $l_1 = l_2$. This is the case you have found, in which case $T_1 = T_2 = \sqrt{(I_{CM} + M l_1^2)/M g l_1}$.

To get an accurate measurement of $g$, you want to be in the first case. So an effective version of Kater's pendulum needs to be designed such that $l_1 \neq l_2$. You can see this from the equation given in the Wikipedia article: $$ g=\frac{8\pi^2}{\dfrac{T_1^2+T_2^2}{\ell_1+\ell_2}+\dfrac{T_1^2-T_2^2}{\ell_1-\ell_2}} $$ Even if the difference in the periods is small ($T_1 \approx T_2$), if $\ell_1 \approx \ell_2$ it can still make a significant difference in your measurement of $g$. So an practical version of Kater's pendulum will be designed so that the CM is much closer to one of the knife edges than the other, eliminating this possibility.

Eli
  • 13,829
Michael Seifert
  • 54,357
1

Kater’s pendulum consists of a rigid metal bar with two knife edges (A and B) placed at different distances from the center of mass. The bar has adjustable weights to fine-tune the center of oscillation.

According to the Kater’s Pendulum Theory, if the time period about both knife edges is the same, the distance between them is equal to the equivalent simple pendulum length $~l~$, which allows for accurate determination of g.

enter image description here

Lets look at the equations .

the equation of motion for small magnitude $~\phi~$

pivot A

$$ I_a\,\ddot \phi+m\,g\,s_a\phi=0 \quad \Rightarrow \\T_a=2\,\pi\sqrt{\frac{I_a}{m\,g\,s_a}}$$

pivot B

$$ T_b=2\,\pi\sqrt{\frac{I_b}{m\,g\,s_b}}$$ where $$ I_a=I_s+m\,s_a^2\quad,I_b=I_s+m\,s_b^2$$

with

$$ s_a+s_b=l$$

and the requirement that $~T_a=T_b~$ you obtain the solution: $$l=\frac{I_s+m\,s_a^2}{m\,s_a}\\ s_b=\frac{I_s}{m\,s_a}$$

this means that if $~T_a=T_b~$ the period $$ T_a=T_b=T=2\,\pi\sqrt{\frac {l}{g}}\quad\Rightarrow $$ $$g=4\,\pi^2 \frac{l}{T^2}\tag 1 $$

Experiment

The pendulum is suspended from the knife edge A, and its time period $~T_A~$ is measured. The pendulum is then inverted and suspended from knife edge B, and its time period $~T_B~$ is measured. The position of adjustable weights is fine-tuned until $~T_A=T_B~$

enter image description here

the period $~T~$ and the The distance $~l~$ between the two knife edges is measured accurately. with T and $~l~$ you can obtain g.

the solution of

$$ s_{{a}}+s_{{b}}-l=0,\\ {\frac {I_{{s}}+m{s_{{a}}}^{2}}{mgs_{{a}}}}-{\frac {I_{{s}}+m{s_{{b}}} ^{2}}{mgs_{{b}}}} =0$$

for l and $~s_b~$ is:

$$ l=2\,s_a~,s_b=s_a $$ this solution means that the center of mass is at $~l/2~$ which is not our case

and $$l=\frac{I_s+m\,s_a^2}{m\,s_a}\quad,s_b=\frac{I_s}{m\,s_a}$$

Equation (1)

$$ 4\,\pi^2\frac{l}{T^2}\overset{?}{=}\,g$$

with \begin{align*} &T_b^2=T^2=4\,{\pi}^{2}\,{\frac { \left( I_{{s}}+m{s_{{b}}}^{2} \right) }{mgs_{{b}}}}\bigg|_{s_b=\frac{I_s}{m\,s_a}}\quad\Rightarrow\\ &4\,\pi^2\,\frac{l}{T^2}=\left(\frac{I_s+m\,s_a^2}{m\,s_a}\right)\, \left(\frac{m\,g\,s_b}{\left( I_{{s}}+m{s_{{b}}}^{2} \right)}\right)\bigg|_{s_b=\frac{I_s}{m\,s_a}}=g \end{align*}

Eli
  • 13,829