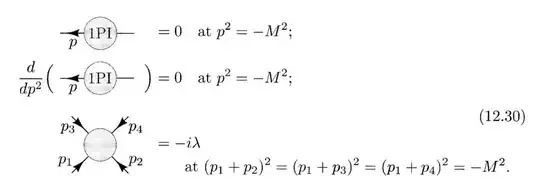Sorry for posting nearly duplicated question (previous post). But I will add some personal understanding (attempts).
In P&S QFT, the massless limit of $\phi^4$ theory was studied in Chapter 12.2. And in equation (12.30), they proposed the following renormalization condition:
My question is that, since the physical mass $m$ is taken to zero, is it necessary that the 1PI function also satisfies some condition at $p^2 = 0$? For example, the full propagator:
$$ G^{(2)}(p) = \frac{i}{p^2 - \Pi(p^2)} $$
Where $-i\Pi(p^2)$ is the 1PI function(eqn (10.26) in P&S, but I use another notation). Since $m$ is the physical mass, then spectral representation tells us that $G^{(2)}(p^2)$ has a pole at $p^2 = m^2 = 0$ and the residue is $i$ at the pole. Then we must have $\Pi(0) = 0$ and $\frac{\mathrm{d}}{\mathrm{d}p^2}\Pi(0) = 0$. But this cannot be true since we have defined $\Pi(p^2)$ at another scale $M$. What's the problem?(That exactly what the previous post asked)
My attempt is as follows:
To resolve this problem, we cannot think $m$ as physical mass(which P&S declare in their book), it is something just like the MS or $\overline{\text{MS}}$ mass which is of no physical meaning(see e.g. this post and also Schwartz's QFT and SM chapter 18.5 for the discussion of the relation between MS mass $m_{\text{MS}}$ and physical pole mass $m_P$). The physical(pole) mass is then defined by the pole of the full propagator $G^{(2)}$, which can be solved if we obtained an expression of $\Pi(p^2)$.
Well, then, what's the physical meaning of setting $m = 0$ since $m$ has no physical meaning?
Then I found that in Coleman's lecture note, he mentioned that when we study the massless limit, we are actually asking how the theory behaved in extremely high energy. The high-E theory mimics the massless theory. And, Schwartz also mentioned that typically, the MS mass and the physical mass differs not too much(Chapter 18.5). Then by setting $m = 0$ in the calculation, we are effectively focusing on the high-E region, which is then equivalent to setting $m_P = 0$?
I'm a self-learner and I don't know whether my understanding is true or not. Are there some evidences (some simple calculations) to prove it?