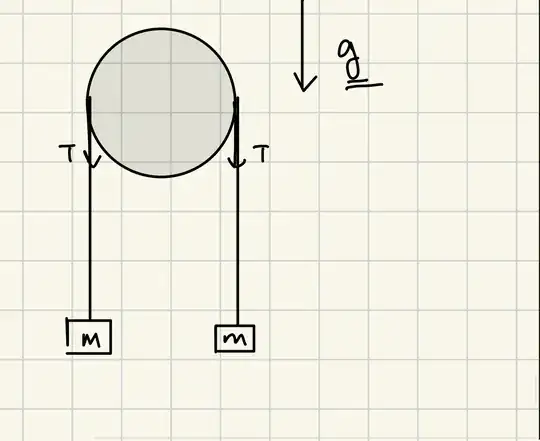
Suppose a situation as shown in figure where pulley (massless) is not fixed to anything and two bodies (initially kept at rest) are joined by a massless rope and then released since gravitational force acts on the masses tension will develop in the string which will pull the pulley down but pulley being massless should not have a net force, so what eventually happens to the pulley? And how does the net force goes zero?
You cannot use Newton’s 2nd law to find the acceleration of a massless object. $\Sigma \vec F = m \vec a$ for $m=0$ yields $\Sigma \vec F=0$ for all $\vec a$.
Instead, $\vec a$ must be determined through some constraint. In this case, the constraint that the length of the rope doesn’t change leads to $a=g$. The net force required for this acceleration is $0$.
You can use Newton’s 2nd law on a massless object to find the net force. Almost trivially $\Sigma \vec F=0$.
The concept of a massless pulley is used when there is a situation when the mass of the pulley is much less than any other mass in the system being considered.
In this case this means that the mass of the pulley is to be taken to be much less than 2m.
Thus the best one can do is apply N2L, with down as positive, to the two masses $mg - T = ma$ and to the pulley $2T + m_{\rm pulley} g = m_{\rm pulley} a$, noting the assumption that the acceleration of each of the objects $a$ is the same.
Combining the two equations gives a non-physical result, $a=\dfrac{2m-m_{\rm pulley}}{2m+m_{\rm pulley}}\cdot g$, with the acceleration of the components of the system being less than $g$ although they are all in free-fall.
Going back to the equations of motion we need to make the tension $T=0$ and then all components accelerate with an acceleration $g$.
Having done all this we can now look at the motion of the pulley again.
If the mass of the pulley is zero, and therefore is not affected by the gravitational force due to the earth, the pulley will be constrained by the massless??!! and inextensible??!! string to have an acceleration of $g$.
A "massless rope" is not actually massless. It is an approximation made that makes things simpler (i.e., that there is a uniform tension in the rope). The approximation generally works when the mass of the rope is significantly smaller (a factor of 10? 100? smaller, depending on the desired accuracy of the calculations) than the mass of the objects it's attached to.
Every good approximation breaks down in certain cases, and you're running into a situation where the "massless rope" approximation breaks down. The fact is, of course that rope has some mass, and so of course it experiences a gravitational force downwards given by $m_{\mathrm{rope}}g$ (provided we're near the surface of the Earth - another approximation). Thus, every object in this system experiences a gravitational force downwards (and no other forces), so all objects are in free fall, accelerating downward with magnitude $g$. The tension in the rope is therefore zero.
Any massless object can be interpreted in two ways:
This law came from the experiments and observation of scientists that came before Newton. (see How did Newton discover his second law?)
By no means were any of the objects these experiments and analyses considered massless!. So now for your case
from the center of mass equation
$$ R_{\rm cm}=\frac {m_p\,r_p+2\,m\,r_m}{M}$$
you obtain the acceleration of the Com :
$$ M\,g=m_p\,g+2\,m a $$
with $~M=m_p+2\,m $
$$ (m_p+2\,m)\,g=m_p\,g+2\,m a\quad \Rightarrow a=g $$
from the Newton's law
$$ m\,a=-m\,g+T\quad \Rightarrow T=2\,m\,g $$
which is wrong . The tension T must be zero !
for a fixed (rotate) pulley
with the free body diagram
$$ m\,a_L=-m\,g+T\\ m\,a_R=-m\,g+T$$
and due to the pulley rotation
$$ a_L=-a_R $$
with those 3 equations you obtain
$$ a_L=a_R=0\\ T=m\,g$$
