Why is redshift possible if the speed of light is constant?

Question

In high school, it is explained to students that the Doppler effect causes the frequency of sound waves to increase during motion towards the sound source, and decrease when moving away.

This explanation is also applied to light waves, to explain the phenomenon of redshift and blueshift.

However, when studying special relativity, I find that the speed of light is invariant, so it should be the same, regardless of the motion of the observer. It is never possible for a body to catch up with its own light waves, as in sound waves. As a result, the frequency of light should be the same. So how can blue/redshift occur?

Answer 1

The speed of light is the same. Its frequency is not.

The equivalent explanation is that, if I hold a laser towards you while moving away at relativistic speed on my rocket, my clock will appear to tick slower than yours, as expected. Then, both due to my motion and the relativistic effects of time dilation, the wavelength of light that I observe to correspond to 650 nm coming out of my laser will be less than the wavelength you observe.

You can also draw out the crests/troughs of the electromagnetic wave for a receding wave source. At that point, even if you let the speed of the wavefront be constant, you see redshift/blueshift from the Doppler effect.

Answer 2

Your question includes a diagram, and the diagram shows that, in the frame of the telescopes, there has to be a Doppler shift of the wavelength, simply because successive spherical wave fronts are not concentric. They spread out from different points as the source moves.

Since $c$ is fixed, and $\lambda$ gets shifted, it follows that $f=c/\lambda$ must get shifted (in the opposite direction).

It is never possible for a body to catch up with its own light waves, as in sound waves.

In the frame of reference of the telescopes, the source doesn't completely catch up with its own light waves that it emitted in the forward direction. However, it does partially catch up with them in that frame, in the sense that it is not as far behind them as it would have been if it had been at rest.

Not being able to catch up with your own light waves (in a vacuum) is a reason why we can't get anything analogous to a sonic boom with light, in a vacuum, but that doesn't mean there can't be Doppler shifts. And in fact a source in a medium can catch up to its own light waves, which is why we get Cherenkov radiation.

Answer 3

Doppler effect from Lorentz transforms: $$\Delta x'=\lambda'=\gamma(1\pm \frac{v}{c})\Delta x=\gamma(1\pm \frac{v}{c}) \lambda \;\;\;\;\;\;\;\; \;\;\;\;\;\;\;\;(1)$$

$$\Delta t'=T'=\gamma(1\pm \frac{v}{c})\Delta t=\gamma(1\pm \frac{v}{c})T\;\;\;\;\;\;\;\; \;\;\;\;\;\;\;\;(2)$$

$(1)/(2)=\frac{\lambda'}{T'}=\frac{\lambda}{T}=c$

so the speed of light is constant in both frames of reference.

Answer 4

If it helps, consider the light source as emitting a single photon every second. If the source is not moving you would expect the distance between photos (frequency) would be one light second. If the source is moving the distance would be one light second +- the difference in velocity. This of course also means that the time it would take to receive those emissions would change accordingly.

Answer 5

The root of your misunderstanding is this: light is not a point particle, and it is not emitted or absorbed instantaneously.

A basic principle of waves is that it takes a non-zero amount of time for one wave cycle to complete. As a result, the wave-front starts travelling towards the receiver before the wave-tail (for lack of a better word) has even been generated. You can see this just by dipping your hand in a body of water - the crest immediately starts travelling out away from your hand as soon as you begin to plunge your hand, before you have even completed the hand-plunge, and well before you have actually finished withdrawing your hand again which finalises the trough of the full wave cycle.

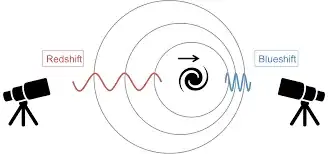
The Doppler principle is that, when the emitter is moving, the front of the wave is emitted in a different place to the tail (or back-end) of the wave. Therefore, you're no longer measuring from a fixed emission point to a fixed reception point - you're measuring an emission that began in one place and finished in another, relative to a fixed reception point.

The faster the emitter moves, the larger this discrepancy becomes between the place where the wave-front began and the place where the wave-tail is finalised.

The constant speed of light relates to the speed of the wave-front, not to the speed of transmission and reception of the full cycle. Under redshift, the latter speed does in fact slow down - under blueshift, it speeds up.

Answer 6

The frequency is the same, but the phase at the receiver location varies with the transmitter distance. For the observer the phase change is undistinguishable from a frequency shift.

The phase of a sine signal is the angle of a rotating vector (phasor). The instantaneous amplitude of the signal is the sine of this angle times the (constant) vector length: $a = sin(\omega t + \varphi)$, $\varphi$ being the phase at $t=0$.

Taken from aviation.se. See also Wikipedia.

Compare with the frequency of a siren when the vehicle moves, the frequency is constant (transmitter attribute). However the wavefront must travel to reach the observer, the phase at the observer location depends on the travel time, hence on the distance. If the distance changes, the phase at the observer location also changes.

Answer 7

I think of it from the frame of reference of the photon. When the photon is emitted, it is a frequency f. When it is absorbed with no relative motion between emitter and absorber, it is still at the same frequency. But if its absorber is moving toward or away from the direction of emission of the photon, the photon can add more or less energy to the absorbing system. (Think of throwing a tennis ball at an approaching car and a receding car.) The photon hasn't changed, but the energy it deposits is different, it is as if the photon were a different wavelength.

This independent of the speed of light, as long as it's finite. Keep in mind, the photon is emitted at t naught, experiences no time passing, and it is absorbed the same instant, t naught. So it has no time to change from its reference frame!