When doing derivation of the electric field between a capacitor, my textbook draws a gaussian surface going through the top plate and going through the space in-between. Then, it calculates the electric field, $E_0=\frac{q}{\epsilon_0 A}$, and calls that the electric field between a capacitor (with no dielectric inserted).
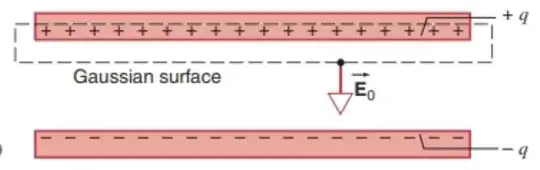
However, in my understanding the electric field counted by the flux only includes the electric field due to the charge enclosed. So $E_0$ only includes the electric field created by the charges in the top plate.
Thus, Shouldn't we have to double our answer to include the electric field created due to the bottom plate?
Hoping someone can resolve this confusion.
