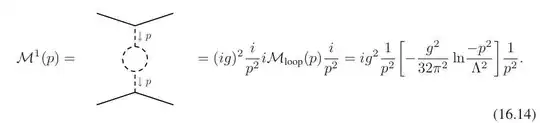Charge renormalization and wavefunction renormalization in QED

Question

In QED, we usually say that charge renormalization is a consequence of vacuum polarization, because of the virtual electron-position pairs, the bare charge is shielded. It is intuitively comprehensible, and we could do calculation based on this fact. On p.303 in Schwartz's QFT and SM, he calculated the electron scattering cross-section with a vacuum polarized photon propagator, and renormalize $e_0$ to $e_R$ to eliminate the infinity.

1. But latter, while developing the renormalized perturbation theory, the photon propagator is made finite by photon field $A_\mu$ redefinition, and charge renormalization (coupling constant renormalization) is achieved by studying the electron-photon vertex. He commented on this difference by "physical results do not care how the infinities are removed"(Page 345). I just can't understand why this is true.

2. Schwartz also noted that in QED, $Z_1 = Z_2$, "this explains why we were able to calculate the renormalization of the electric charge from only the vacuum polarization graphs"(Page 351). So the key point is $Z_1 = Z_2$? If I had another theory, let's say a $\phi^3$ theory $$\mathcal{L} = \frac{1}{2}(\partial_\mu \phi)^2 - \frac{1}{2} \mu^2 \phi^2 + \frac{g}{3!} \phi^3,\tag{16.3}$$ can I do the same thing? I mean for this $\phi^3$ theory, can we just calculate vacuum polarization diagram to get the coupling constant renormalization?

Answer 1

1. OP's 1st question is essentially a duplicate of e.g. this & this Phys.SE questions.

2. On one hand, vacuum polarization/self-energy diagrams yield wavefunction renormalization, such as e.g. $Z_{\psi}\equiv Z_2$ and $Z_A\equiv Z_3$ in QED and $Z_{\phi}$ in $\phi^3$-theory) and mass renormalization.

   On the other hand, coupling constant renormalizations, such as e.g.$$\frac{e_0}{e\tilde{\mu}^{\varepsilon/2}}~=~\frac{Z_e}{Z_A^{1/2}Z_{\psi}}~\equiv~\frac{Z_1}{Z_3^{1/2}Z_2}~=~Z_3^{-1/2}\tag{66.1}$$ in QED, and $$\frac{g_0}{g\tilde{\mu}^{\varepsilon/2}}~=~\frac{Z_g}{Z_\phi^{3/2}}\tag{28.5}$$ in $\phi^3$-theory, are given by 1PI vertex functions, cf. Ref. 1

   In QED, one can determine the coupling constant renormalization (66.1) from the photon vacuum polarization $Z_A\equiv Z_3$ due to the identity $Z_1=Z_2$, which is a consequence of gauge symmetry. This is not possible in $\phi^3$-theory (28.5), cf. OP's question.

References:

1. M. Srednicki, QFT, 2007; eqs. (28.5) & (66.1). A prepublication draft PDF file is available here.

Answer 2

1). "physical results do not care how the infinities are removed"

If you have a physical observable/measurement, the outcome of that measurement is objective. The way you choose to turn an unphysical quantity into a physical quantity should therefore not yield different physical results, because the outcome of the measureable should be objective. This is also true when you have to choose a gauge - the physical result does not care about how it is calculated.

2). "So the key point is $Z_1=Z_2$?"

That $Z_1=Z_2$ is the key point of this chapter. It implies that the ratios between charges are fixed to all orders, and does not receive any radiative corrections - e.g. the charge of the electron and positron are always exactly opposite despite having very different interactions.

The fact that $Z_1=Z_2$ in QED is only true for certain renormalization-schemes. Schwartz comments on this (p.353, between Eq. 19.82 and 19.83):

"Note, however, that one can choose a more exotic subtraction scheme in which $Z_1=Z_2$ does not hold."

3). "If I had another theory, let's say a $\phi^3$ theory $\mathcal{L}=\frac{1}{2}(\partial_\mu\phi)^2−\frac{1}{2}\mu^2\phi^2+\frac{g}{3!}\phi^3$ , can I do the same thing?"

Same thing in what sense? There is no gauge-interactions in $\phi^3$-theory, so there is no charge-renormalization. You can renormalize the mass $\mu$, the coupling $g$ and the field $\phi$, but there is (as far as I can see immediately) no special reason that you should expect $Z_1=Z_2$ in $\phi^3$. But on p. 302 in Schwartz, you can read more about renormalization and $\phi^3$-theory. I encourage you to try to renormalize $\phi^3$ and check yourself if $Z_1=Z_2$, but I unfortunately do not have the time myself.