Derivation of Euler force

Question

I was studying the Coriolis force and subsequently non-inertial reference frames. I see that the "Formula" section for Coriolis force wikipedia article contains the formula $$\vec{F}' = \vec{F} - m \frac{d\vec{\omega}}{dt} \times \vec{r}'- 2m \vec{\omega} \times \vec{v}' - m\vec{\omega} \times (\vec{\omega} \times \vec{r}'),$$ where the $(')$ indicates the vector is the vector being in the rotating reference frame, otherwise it is in the inertial reference frame. Where does the Euler force $-m\frac{d\vec{\omega}}{dt} \times \vec{r}'$ come from?

I read up on this question on this forum with the derivation of how to go from an inertial reference frame to a rotating one. However, it does not include the Euler force. Maybe someone can follow-up on this otherwise good derivation?

Answer 1

The mathematical derivation of the Euler force is shown in many textbooks and webpages, eg Rotating Frames.

For a more arm-waving approach consider a mass $m$ at rest relative to turntable rotating at a constant angular velocity $\vec \omega = w\,\hat \omega$ at a constant position $\vec r = r \, \hat r$ from the axis of rotation, as shown in the diagram below.

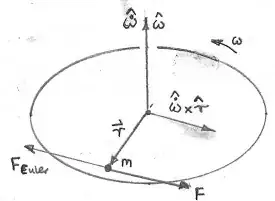
The magnitude of the centripetal force on the mass due to the turntable is $m\,r\,\omega^2$ and its direction is towards the axis of rotation.
To an observer standing on the turntable there is net force on the mass yet it is not accelerating relative to the observer.
So that Newton's laws can be used in the rotating frame F = an extra fictitious force (centrifugal force) of the same magnitude as the centripetal force but opposite in direction is applied to the mass so that the net "force" on the mass is zero.

Now suppose that the magnitude of the angular velocity is changing.
This means that the velocity of the mass must increase and the magnitude of its acceleration is $\vec r$ is $r\,\dot\omega$ (by differentiating $v=r\,\omega$) in a direction perpendicular to $\vec r$, $\,\hat{\dot \omega}\times \hat r$ as shown in the diagram.
To achieve this acceleration the turntable must exert a force $m\, (\vec{\dot \omega}\times \vec r)$ on the mass.

An observer standing and on the platform notes that there is force $m\, (\vec{\dot \omega}\times \vec r)$ acting on the mass but the mass is not moving.
To use Newton's laws in the rotating frame an extra (fictitious) force, $\vec F_{\rm Euler}=-m\, (\vec{\dot \omega}\times \vec r)$, is applied to the mass so that the net "force" on the mass is again zero.

The third fictitious force, the Coriolis force, "appears" when the mass is moving relative to the turntable.

Again using "arm-waving" to illustrate the origin ogf the two fictitious forces which make up the Coriolis force.

Imagine a railway track from position $A$ to position $O$ which is the centre of a large rotating turntable and rotating at angular velocity $\omega$.

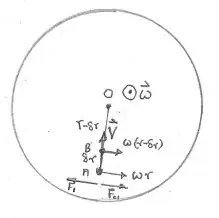
As a train travels from $A$ to $B$, separation $\delta r$, towards the centre of the turntable at velocity $\vec V$ the magnitude of its velocity to the right, (at right angles to $\vec V$), changes from $\omega\, r$ to $\omega\, (r-\delta r)$.
Thus the magnitude of its change in velocity to the left is $\omega \,r - \omega\, (r-\delta r)= \omega \,\delta r$.
$\delta r = V \delta t \Rightarrow {\rm acceleration}_{\rm left}= \dfrac{\omega \cdot V \delta t}{\delta t}= \omega \,V$ in the direction $\hat \omega \times \hat V$.
Thus the force acting in the train to keep it moving along the rails is $\vec F_1=m\,\vec \omega \times \vec V$.
For a person standing on the turntable the train is not accelerating and so a fictitious force $\vec F_{\rm C1} = - m\,\vec \omega \times \vec V$ is introduced.

The second contribution to the Coriolis force is due to the fact that the direction of the rails and hence the train change with time as shown in the left-hand diagram below.

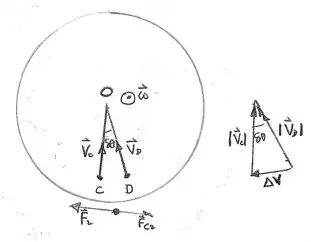
The train's velocity vector diagram is shown on the right-hand side with $|\vec V_{\rm C}|= |\vec V_{\rm D}| = V$. The magnitude ogf the change in velocity $\delta V = V\delta \theta = V\,\omega\,\delta t$.
Thus the force acting on the train due to the rails is $F_2=m \,\dfrac{V\,\omega\,\delta t}{\delta t}= m\,V\,\omega$ in the direction $\hat \omega \times \hat V$.
The second contribution to the Coriolis force is $\vec F_{\rm C2} = - m\,\vec \omega \times \vec V$

Answer 2

$\def \c {\boldsymbol} \def \p {\dot} \def \pp {\ddot} \def \b {\mathbf}$

Newton second law is: \begin{align*} &m\,\b{\ddot{r}}=\b F \end{align*} where the components of the acceleration $~\b{\ddot{r}}$ and the external force $~\b F~$ are given in inertial frame.

form here, the Newton second law in components of the body frame

\begin{align*} &m\,\b S^T\,\b{\ddot{r}}=\b S^T\,\b F\tag 1 \end{align*}

where $~\b S~$ is the transformation matrix between body and inertial frame .

Lets calculate $~\b S^T\,\b{\ddot{r}}~$

stating with the position vector $~\b r~$ \begin{align*} &\b r=\b S \,\b p\quad\text{where}~\b p ~\text{is the CoM vector given in body frame}\quad\Rightarrow\\ &\b{\dot{r}}=\b{\dot{S}}\,\b p+\b S\,\b{\dot{p}}\\ &\b{\ddot{r}}= \b{\ddot{S}}\b p+\b{\dot{S}}\,\b{\dot{p}}+\b{\dot{S}}\,\b{\dot{p}}+\b S\b{\ddot{p}} \end{align*} with \begin{align*} &\b{\dot{S}}=\b S\,\c\Omega\\ &\b{\ddot{S}}=\b{\dot{S}}\,\c\Omega+\b S\c{\dot{\Omega}} =\b S\,\c\Omega\,\c\Omega+\b S\c{\dot{\Omega}} \end{align*} thus the acceleration $~\b{\ddot{r}}~$ \begin{align*} &\b{\ddot{r}}=\left(\,\b S\,\c\Omega\,\c\Omega+\b S\c{\dot{\Omega}}\,\right)\,\b p+ 2\,\b S\,\c\Omega\b{\dot{p}}+\b S\b{\ddot{p}} \end{align*} and Eq. (1)

\begin{align*} &m\,\b S^T\,\underbrace{\left[\left(\b S\,\c\Omega\,\c\Omega+\b S\c{\dot{\Omega}}\right)\,\b p+ 2\,\b S\,\c\Omega\b{\dot{p}}+\b S\b{\ddot{p}}\right]}_{\b{\ddot{r}}}=\b S^T\,\b F \end{align*} or \begin{align*} m\,\b{\ddot{p}}=\b F_b-\underbrace{m\,\left(\c\omega\times\c\omega\times\b p +2\,(\c\omega\times\b{\dot{p}})+\c{\dot{\omega}}\times \b p\right)}_{\rm Fictitious forces} \end{align*}

---

• $\c\Omega=\left[ \begin {array}{ccc} 0&-\omega_{{z}}&\omega_{{y}} \\ \omega_{{z}}&0&-\omega_{{x}}\\ -\omega_{{y}}&\omega_{{x}}&0\end {array} \right]$